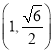题目内容
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,左右顶点分别是
轴上,左右顶点分别是![]() ,以
,以![]() 上的弦
上的弦![]() (
(![]() 异于
异于![]() )为直径作圆
)为直径作圆![]() 恰好过
恰好过![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() .
.
(1)若![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的方程.
的方程.
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)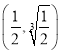
【解析】
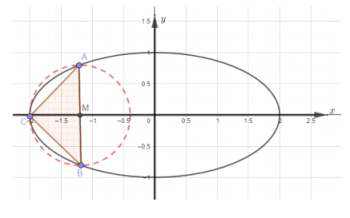
(1)已知圆![]() 恰好过左顶点
恰好过左顶点![]() ,则
,则![]() ,又
,又![]() ,于是
,于是![]() ,故
,故![]() 是等腰直角三角形,且可看作两个全等的直角三角形拼接而成,而两直角三角形恰好可以组成一个以
是等腰直角三角形,且可看作两个全等的直角三角形拼接而成,而两直角三角形恰好可以组成一个以![]() 边长的正方形,根据面积可得
边长的正方形,根据面积可得![]() 的坐标,再代入方程可求得
的坐标,再代入方程可求得![]() 的值,即可得答案;
的值,即可得答案;
(2)由![]() ,得
,得![]() ,可得
,可得![]() ,从而求得
,从而求得![]() 的取值范围.
的取值范围.
(1)已知圆![]() 恰好过左顶点
恰好过左顶点![]() ,则
,则![]() ,又
,又![]() ,于是
,于是![]() ,故
,故![]() 是等腰直角三角形,且可看作两个全等的直角三角形拼接而成,而两直角三角形恰好可以组成一个以
是等腰直角三角形,且可看作两个全等的直角三角形拼接而成,而两直角三角形恰好可以组成一个以![]() 边长的正方形
边长的正方形
又![]() ,解得
,解得![]() ,
,
代入方程![]() ,得
,得![]() ,解得
,解得![]()
所以![]() ,即
,即![]() ,解得
,解得![]()
所以![]() 的方程是
的方程是![]() .
.
(2)由![]() ,得
,得![]() ,
,
联立方程 ,得
,得![]() ,
,
设其两个根是![]() ,由韦达定理,得
,由韦达定理,得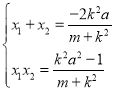 ,
,
则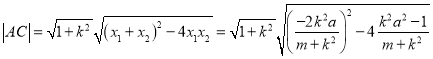
![]() ,
,
将![]() 换成
换成![]() ,得
,得
从而![]() ,即
,即![]()
故![]() ,因此
,因此![]() ,解得
,解得![]() ,
,
故![]() 的取值范围是
的取值范围是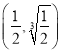 .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】某工厂计划建设至少3个,至多5个相同的生产线车间,以解决本地区公民对特供商品![]() 的未来需求.经过对先期样本的科学性调查显示,本地区每个月对商品
的未来需求.经过对先期样本的科学性调查显示,本地区每个月对商品![]() 的月需求量均在50万件及以上,其中需求量在50~ 100万件的频率为0.5,需求量在100~200万件的频率为0.3,不低于200万件的频率为0.2.用调查样本来估计总体,频率作为相应段的概率,并假设本地区在各个月对本特供商品
的月需求量均在50万件及以上,其中需求量在50~ 100万件的频率为0.5,需求量在100~200万件的频率为0.3,不低于200万件的频率为0.2.用调查样本来估计总体,频率作为相应段的概率,并假设本地区在各个月对本特供商品![]() 的需求相互独立.
的需求相互独立.
(1)求在未来某连续4个月中,本地区至少有2个月对商品![]() 的月需求量低于100万件的概率.
的月需求量低于100万件的概率.
(2)该工厂希望尽可能在生产线车间建成后,车间能正常生产运行,但每月最多可正常生产的车间数受商品![]() 的需求量
的需求量![]() 的限制,并有如下关系:
的限制,并有如下关系:
商品 |
|
|
|
车间最多正常运行个数 | 3 | 4 | 5 |
若一个车间正常运行,则该车间月净利润为1500万元,而一个车间未正常生产,则该车间生产线的月维护费(单位:万元)与月需求量有如下关系:
商品 |
|
|
未正常生产的一个车间的月维护费(万元) | 500 | 600 |
试分析并回答该工厂应建设生产线车间多少个?使得商品![]() 的月利润为最大.
的月利润为最大.