题目内容
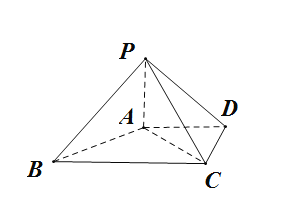
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(1)证明:![]() .
.
(2)若![]() ,试在棱
,试在棱![]() 上确定一点
上确定一点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【答案】(1)证明见解析;(2)点![]() 为棱
为棱![]() 的中点
的中点
【解析】
(1)在同一平面内用数据说话证明 ![]() ,利用
,利用![]() 平面
平面![]() ,证明
,证明![]() ,
,
从而得证![]() 平面
平面![]() ,得到
,得到![]() .
.
(1)取![]() 的中点
的中点![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,使用空间向量求
为坐标原点建立空间直角坐标系,使用空间向量求![]() 及平面
及平面![]() 的一个法向量
的一个法向量![]() ,利用夹角公式求解即可.
,利用夹角公式求解即可.
(1)证明:∵![]() ,且
,且![]() ,∴
,∴![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
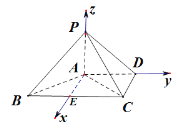
(2)解:取![]() 的中点
的中点![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .如图所示.
.如图所示.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,
则![]() .
.
由(1)可知,![]() 平面
平面![]() ,∴
,∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
则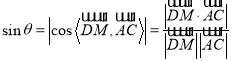
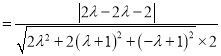
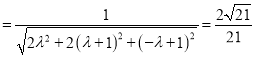 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
∴点![]() 为棱
为棱![]() 的中点.
的中点.

练习册系列答案
相关题目
【题目】某医院对治疗支气管肺炎的两种方案![]() ,
,![]() 进行比较研究,将志愿者分为两组,分别采用方案
进行比较研究,将志愿者分为两组,分别采用方案![]() 和方案
和方案![]() 进行治疗,统计结果如下:
进行治疗,统计结果如下:
有效 | 无效 | 合计 | |
使用方案 | 96 | 120 | |
使用方案 | 72 | ||
合计 | 32 |
(1)完成上述列联表,并比较两种治疗方案有效的频率;
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
附: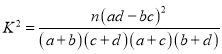 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |