题目内容
10.设x,y∈R,满足$\left\{\begin{array}{l}{(x-1)^{5}+2x+sin(x-1)=3}\\{(y-1)^{5}+2y+sin(y-1)=1}\end{array}\right.$,则x+y=( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
分析 根据条件,构造函数f(t)=t5+2t+sint,利用函数f(t)的奇偶性和单调性解方程即可.
解答 解:∵(x-1)5+2x+sin(x-1)=3,
∴(x-1)5+2(x-1)+sin(x-1)=3-2=1,
∵(y-1)5+2y+sin(y-1)=1,
∴(y-1)3+2(y-1)+sin(y-1)=1-2=-1,
设f(t)=t5+2t+sint,
则f(t)为奇函数,且f'(t)=5t4+2+cost>0,
即函数f(t)单调递增.
由题意可知f(x-1)=1,f(y-1)=-1,
即f(x-1)+f(y-1)=1-1=0,
即f(x-1)=-f(y-1)=f(1-y),
∵函数f(t)单调递增
∴x-1=1-y,
即x+y=2,
故选B.
点评 本题主要考查函数奇偶性和单调性的应用,利用条件构造函数f(t)是解决本题的关键,综合考查了函数的性质.

练习册系列答案
相关题目
18.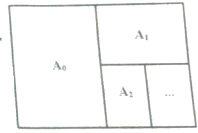 An(n∈N)系列的纸张规格如图,其特点是
An(n∈N)系列的纸张规格如图,其特点是
①A0,A1,A2,…An所有规格的纸张的长宽比都相同;
②A0对裁后可以得到两张A1,A1对裁后可以得到两张A2,…,An-1对裁后可以得到两张An;
若梅平方厘米重量为b克的A0,A1,A2,…An纸张各一张,其中A4纸较短边的长为a厘米,记这(n+1)纸张的重量之和为Sn+1,则下列论断错误的是( )
 An(n∈N)系列的纸张规格如图,其特点是
An(n∈N)系列的纸张规格如图,其特点是①A0,A1,A2,…An所有规格的纸张的长宽比都相同;
②A0对裁后可以得到两张A1,A1对裁后可以得到两张A2,…,An-1对裁后可以得到两张An;
若梅平方厘米重量为b克的A0,A1,A2,…An纸张各一张,其中A4纸较短边的长为a厘米,记这(n+1)纸张的重量之和为Sn+1,则下列论断错误的是( )
| A. | 存在n∈N,使得Sn+1=32$\sqrt{2}$a2b | B. | 存在n∈N,使得Sn+1=16$\sqrt{2}$a2b | ||
| C. | 对于任意n∈N,使得Sn+1≤32$\sqrt{2}$a2b | D. | 对于任意n∈N,使得Sn+1≥16$\sqrt{2}$a2b |
5.在四棱锥V-ABCD中,B1,D1分别为侧棱VB、VD的中点,则四面体AB1CD1的体积与四棱锥V-ABCD的体积之比为( )
| A. | 1:6 | B. | 1:5 | C. | 1:4 | D. | 1:3 |
15.在△ABC中,sin2A≥sin2B+sin2C-sinBsinC,则∠A的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{3}$] | C. | [$\frac{π}{6}$,π) | D. | [$\frac{π}{3}$,π) |
2.已知集合={x|1-x>0},B={x|2x>1},则A∩B=( )
| A. | ∅ | B. | {x|0<x<1} | C. | {x|x<0} | D. | {x|x>1} |
19. 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |