题目内容
14.设方程log2x-($\frac{1}{2}$)x=0与log${\;}_{\frac{1}{4}}$x-($\frac{1}{4}$)x=0的根分别为x1,x2,则( )| A. | 0<x1x2<1 | B. | x1x2=1 | C. | 1<x1x2<2 | D. | x1x2≥2 |
分析 由题意画出图形,得到${x}_{2}=\frac{1}{2}$,且得到1<x1<2,由此可得答案.
解答 解:如图,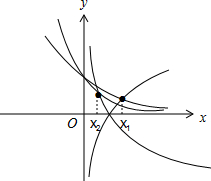
由log${\;}_{\frac{1}{4}}$x-($\frac{1}{4}$)x=0,可得${x}_{2}=\frac{1}{2}$,
当x=2时,$lo{g}_{2}2=1,(\frac{1}{2})^{2}=\frac{1}{4}$,∴1<x1<2.
则$\frac{1}{2}<{x}_{1}{x}_{2}<1$.
故选:A.
点评 本题考查了根的存在性及根的个数判断,以及函数与方程的思想,解答关键是运用数形结合的思想,属于中档题.

练习册系列答案
相关题目
14.设a,b是实数,则“a+b>0”是“ab>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.在四棱锥V-ABCD中,B1,D1分别为侧棱VB、VD的中点,则四面体AB1CD1的体积与四棱锥V-ABCD的体积之比为( )
| A. | 1:6 | B. | 1:5 | C. | 1:4 | D. | 1:3 |
2.已知集合={x|1-x>0},B={x|2x>1},则A∩B=( )
| A. | ∅ | B. | {x|0<x<1} | C. | {x|x<0} | D. | {x|x>1} |
19. 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |