题目内容
4.若a,b∈(0,2),则函数f(x)=$\frac{1}{3}$ax3+2x2+4bx+1存在极值的概率为( )| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1-ln2}{2}$ |
分析 利用导数求得函数有极值的条件,进而转化为几何概型求得概率.
解答 解:f'(x)=ax2+4x+4b
因为函数f(x)存在极值,所以f'(x)=0有解
则△=16-16ab≥0,即ab≤1.
令ab=1,b=$\frac{1}{a}$,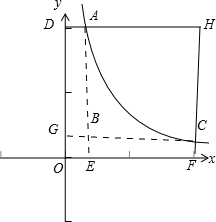
当b=2,a=$\frac{1}{2}$,
当a=2,b=$\frac{1}{2}$,
∴${∫}_{\frac{1}{2}}^{2}\frac{1}{a}-\frac{1}{2}da$=lna-1-ln$\frac{1}{2}$+$\frac{1}{4}$=2ln2-$\frac{3}{4}$
三块小矩形的面积为$2×\frac{1}{2}+\frac{3}{2}×\frac{1}{2}=\frac{7}{4}$,
∴S=2ln2+1,
∴$\frac{S}{{S}_{正}}=\frac{2ln2+1}{4}$,
故选A
点评 主要考查函数有极值的条件和利用几何概型解题的方法.在高考中属常考题型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
15.在△ABC中,sin2A≥sin2B+sin2C-sinBsinC,则∠A的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{3}$] | C. | [$\frac{π}{6}$,π) | D. | [$\frac{π}{3}$,π) |
12.A、B是半径为2的圆O上的两点,M是弦AB上的动点,若△AOB为直角三角形,则$\overrightarrow{OM}$•$\overrightarrow{AM}$的最小值为( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 0 | D. | 2 |
19. 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
9.已知在△ABC中,a、b、c分别是三个内角∠A、∠B、∠C的对边,且$\frac{sinA-sinC}{sinB}$=$\frac{sinA-sinB}{sinA+sinC}$,则∠C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
16.根据如下样本数据得到的回归方程为$\stackrel{∧}{y}$=bx+a.若a=7.9,则x每增加1个单位,y就( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A. | 增加1.4个单位 | B. | 减少1.4个单位 | C. | 增加1.2个单位 | D. | 减少1.2个单位. |