题目内容
已知函数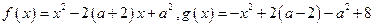 .设
.设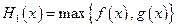 ,
,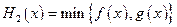 (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记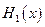 的最小值为A,
的最小值为A,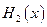 的最大值为B,则
的最大值为B,则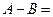 ( )
( )
| A.16 |
B.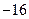 |
C.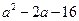 |
D.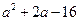 |
B
解析

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
题目内容
已知函数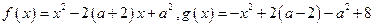 .设
.设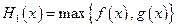 ,
,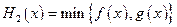 (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记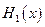 的最小值为A,
的最小值为A,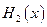 的最大值为B,则
的最大值为B,则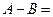 ( )
( )
| A.16 |
B.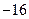 |
C.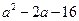 |
D.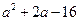 |
B
解析

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案