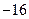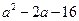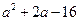题目内容
已知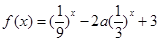
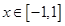
(1)若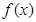 的最小值记为
的最小值记为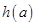 ,求
,求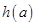 的解析式.
的解析式.
(2)是否存在实数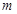 ,
,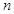 同时满足以下条件:①
同时满足以下条件:① ;②当
;②当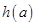 的定义域为[
的定义域为[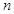 ,
,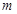 ]时,值域为[
]时,值域为[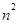 ,
,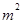 ];若存在,求出
];若存在,求出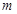 ,
, 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1) 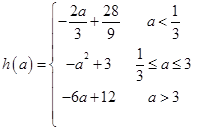 ;(2) 满足条件的实数m,n不存在.
;(2) 满足条件的实数m,n不存在.
解析试题分析:(1)利用换元法令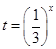 ,可知
,可知 ,原函数化为
,原函数化为 ,利用一元二次函数求最值,可得最小值
,利用一元二次函数求最值,可得最小值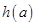 的解析式;(2)由 ①知m>n>3,故
的解析式;(2)由 ①知m>n>3,故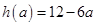 ,由函数的单调性知
,由函数的单调性知
12?6m=n2,12?6n=m2 得m+n=6与m>n>3矛盾,故不存在.
解:(1)令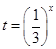 ,∵
,∵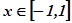 ∴
∴ , 1分
, 1分
 ,对称轴
,对称轴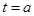 . 2分
. 2分
①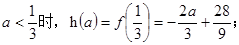
②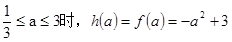 ,
,
③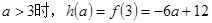 , 5分
, 5分
∴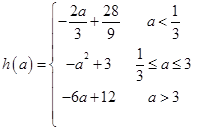 7分
7分
(2)因为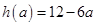 在(3,+∞)上为减函数,而m>n>3,
在(3,+∞)上为减函数,而m>n>3,
∴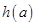 在[n,m]上的值域为[h(m),h(n)], (8分)
在[n,m]上的值域为[h(m),h(n)], (8分)
∵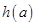 在[n,m]上的值域为[
在[n,m]上的值域为[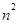 ,
,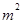 ],
],
∴h(m)=n2, h(n)=m2
即:12?6m=n2 ,12?6n=m2 (9分)
两式相减得:6(m-n)=(m-n)(m+n)
又m>n>3∴m+n=6,而m>n>3时,有m+n>6,矛盾. (12分)
故满足条件的实数m,n不存在. (13分)
考点:换元法,一元二次函数的最值,函数的单调性.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
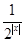 +2.
+2.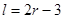 (
(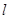 为圆柱的高,
为圆柱的高,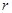 为球的半径,
为球的半径,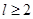 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为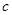 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
 ,其中a为大于零的常数.
,其中a为大于零的常数. +
+ +…+
+…+ 恒成立.
恒成立. 
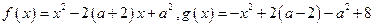 .设
.设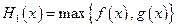 ,
,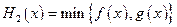 (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记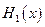 的最小值为A,
的最小值为A,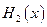 的最大值为B,则
的最大值为B,则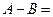 ( )
( )