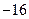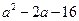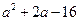题目内容
已知函数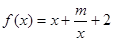 (
(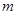 为实常数).
为实常数).
(1)若函数 在区间
在区间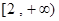 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数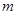 的取值范围;
的取值范围;
(2)设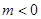 ,若不等式
,若不等式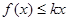 在
在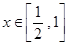 有解,求
有解,求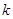 的取值范围.
的取值范围.
(1)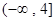 ;(2)当
;(2)当 时,
时,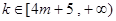 ;当
;当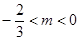 时,
时,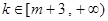 .
.
解析试题分析:(1)任取x1、x2∈[2,+∞),且x1<x2,利用函数单调性的定义可知f(x2)-f(x1)>0在区间[2,+∞)上恒成立,从而求出实数m的取值范围;(2)将不等式f(x)≤kx中的k分离出来,然后利用二次函数的性质研究不等式另一侧函数在[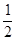 ,1]上的最小值,从而求出k的取值范围.
,1]上的最小值,从而求出k的取值范围.
(1)由题意,任取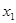 、
、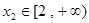 ,且
,且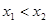 ,
,
则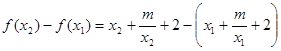
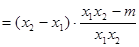
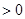 , 2分
, 2分
因为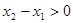 ,
,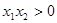 ,所以
,所以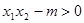 ,即
,即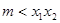 , 4分
, 4分
由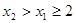 ,得
,得 ,所以
,所以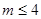 .所以,
.所以,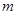 的取值范围是
的取值范围是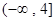 . 6分
. 6分
(2)由 ,得
,得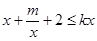 ,
,
因为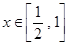 ,所以
,所以 , 7分
, 7分
令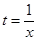 ,则
,则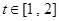 ,所以
,所以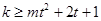 ,令
,令 ,
,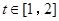 ,
,
于是,要使原不等式在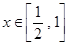 有解,当且仅当
有解,当且仅当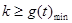 (
(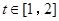 ). 9分
). 9分
因为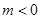 ,所以
,所以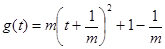 图像开口向下,对称轴为直线
图像开口向下,对称轴为直线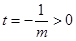 ,
,
因为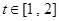 ,故当
,故当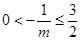 ,即
,即 时,
时, ;
;
当 ,即
,即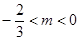 时,
时,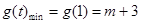 . 13分
. 13分
综上,当 时,
时,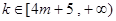 ;
;
当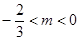 时,
时,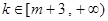 . 14分.
. 14分.
考点:1.不等式的解法;2.奇偶性与单调性的综合;3.两点间的距离公式..

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
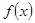 是定义在
是定义在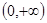 上的函数,且
上的函数,且 ,对任意
,对任意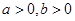 ,若经过点
,若经过点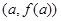 ,
,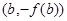 的直线与
的直线与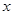 轴的交点为
轴的交点为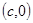 ,则称
,则称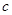 为
为 关于函数
关于函数 ,例如,当
,例如,当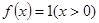 时,可得
时,可得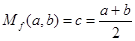 ,即
,即 时,
时, ;
;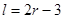 (
(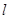 为圆柱的高,
为圆柱的高,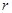 为球的半径,
为球的半径,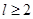 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为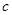 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.

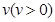 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与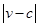 ×S成正比,比例系数为
×S成正比,比例系数为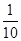 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记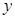 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=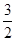 时。
时。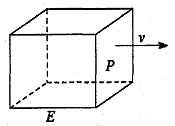
 ,使总淋雨量
,使总淋雨量 (万元)可以看成月产量
(万元)可以看成月产量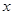 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.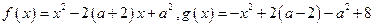 .设
.设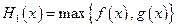 ,
,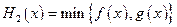 (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记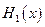 的最小值为A,
的最小值为A,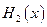 的最大值为B,则
的最大值为B,则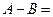 ( )
( )