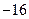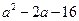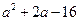题目内容
已知函数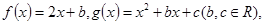 对任意的
对任意的 恒有
恒有 成立.
成立.
(1)当b=0时,记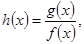 若
若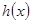 在
在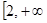 )上为增函数,求c的取值范围;
)上为增函数,求c的取值范围;
(2)证明:当 时,
时,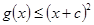 成立;
成立;
(3)若对满足条件的任意实数b,c,不等式 恒成立,求M的最小值.
恒成立,求M的最小值.
(1) ;(2)证明见解析;(3)
;(2)证明见解析;(3)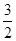 .
.
解析试题分析:(1)首先要讨论题设的先决条件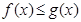 对
对 恒成立,
恒成立,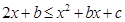 ,即
,即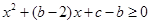 恒成立,这是二次不等式,由二次函数知识,有
恒成立,这是二次不等式,由二次函数知识,有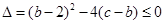 ,化简之后有
,化简之后有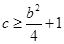 ,从而
,从而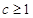 .
.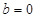 时,
时, 在
在 上是增函数,我们用增函数的定义,即设
上是增函数,我们用增函数的定义,即设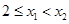 ,
,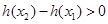 恒成立,分析后得出
恒成立,分析后得出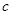 的范围;(2)
的范围;(2)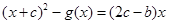
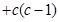 ,问题变成证明
,问题变成证明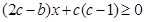 在
在 时恒成立,在
时恒成立,在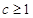 的情况下,
的情况下, ,而
,而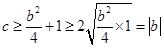 ,可见
,可见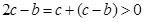 ,那当
,那当 时,一定恒有
时,一定恒有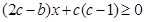 ,问题证毕;(3)由(2)
,问题证毕;(3)由(2)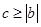 ,在
,在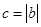 时,
时,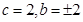 ,这时柺验证不等式
,这时柺验证不等式 成立,当
成立,当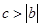 时
时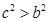 ,不等式可化为
,不等式可化为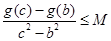 ,因此要求
,因此要求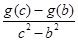 的最大值或者它的值域,
的最大值或者它的值域,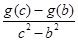
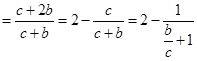 ,而
,而 ,因此
,因此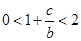 ,由此
,由此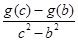 的取值范围易得,
的取值范围易得,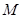 的最小值也易得.
的最小值也易得.
试题解析:(1)因为任意的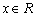 恒有
恒有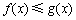 成立,
成立,
所以对任意的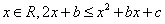 ,即
,即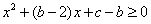 恒成立.
恒成立.
所以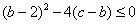 ,从而
,从而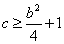 .,即:
.,即: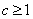 .
.
当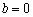 时,记
时,记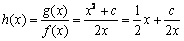 (
(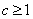 )
)
因为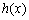 在
在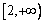 上为增函数,所以任取
上为增函数,所以任取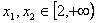 ,
,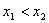 ,
, 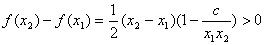 恒成立.
恒成立.
即任取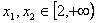 ,
,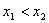 ,
,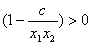 成立,也就是
成立,也就是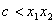 成立.
成立.
所以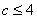 ,即
,即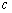 的取值范围是
的取值范围是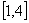 .
.
(2)由(1)得,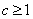 且
且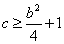 ,
,
所以 ,因此
,因此 .
.
故当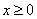 时,有
时,有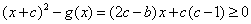 .
.
即当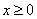 时,
时,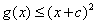 .
.
(3)由(2)知,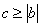 ,
,
当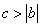 时,有
时,有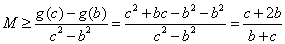

练习册系列答案
相关题目
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①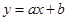 ;②
;②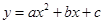 ;③
;③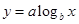 .
.(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格.
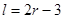 (
(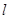 为圆柱的高,
为圆柱的高,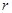 为球的半径,
为球的半径,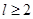 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为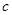 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
 (万元)可以看成月产量
(万元)可以看成月产量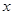 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
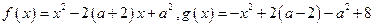 .设
.设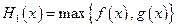 ,
,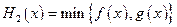 (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记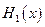 的最小值为A,
的最小值为A,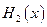 的最大值为B,则
的最大值为B,则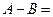 ( )
( )