题目内容
(本小题满分14分)已知函数
(1)若在 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数 的图象与函数
的图象与函数 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.

(1)若在
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;(2)若
 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;(3)在(1)的条件下,是否存在实数m,使得函数
 的图象与函数
的图象与函数 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.(1)a=1;(2)a的取值范围为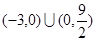
(3)存在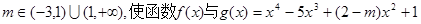 的图象恰有三个交点
的图象恰有三个交点
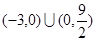
(3)存在
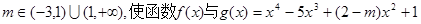 的图象恰有三个交点
的图象恰有三个交点本题主要考查函数与方程的综合运用,主要涉及了方程的根与函数的零点间的转化.还考查了计算能力和综合运用知识的能力.
(1)先求出函数的导数,再由f′(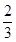 )=0求解a.
)=0求解a.
(2)将“f(x)在区间(-2,3)内有两个不同的极值点”转化为“方程f′(x)=0在区间(-2,3)内有两个不同的实根”,用△>0求解.
(3)在(1)的条件下,a=1,“要使函数f(x)与g(x)=x4-5x3+(2-m)x2+1的图象恰有三个交点”即为“方程x2(x2-4x+1m)=0恰有三个不同的实根”.因为x=0是一个根,所以方程x2-4x+1-m=0应有两个非零的不等实根,再用判别式求解.
解:(1)依题意,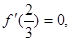
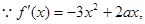
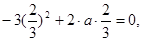
 …………………………3分
…………………………3分
(2)若 在区间(—2,3)内有两个不同的极值点,
在区间(—2,3)内有两个不同的极值点,
则方程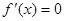 在区间(—2,3)内有两个不同的实根,
在区间(—2,3)内有两个不同的实根,
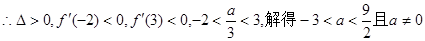
但a=0时,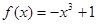 无极值点,
无极值点,
∴a的取值范围为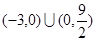
(3)在(1)的条件下,a=1,要使函数 的图象恰有三个交点,等价于方程
的图象恰有三个交点,等价于方程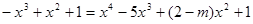 ,
,
即方程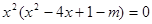 恰有三个不同的实根。
恰有三个不同的实根。
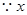 =0是一个根,
=0是一个根,
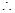 应使方程
应使方程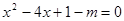 有两个非零的不等实根,
有两个非零的不等实根,
由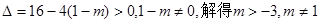
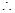 存在
存在 的图象恰有三个交点。
的图象恰有三个交点。
(1)先求出函数的导数,再由f′(
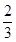 )=0求解a.
)=0求解a.(2)将“f(x)在区间(-2,3)内有两个不同的极值点”转化为“方程f′(x)=0在区间(-2,3)内有两个不同的实根”,用△>0求解.
(3)在(1)的条件下,a=1,“要使函数f(x)与g(x)=x4-5x3+(2-m)x2+1的图象恰有三个交点”即为“方程x2(x2-4x+1m)=0恰有三个不同的实根”.因为x=0是一个根,所以方程x2-4x+1-m=0应有两个非零的不等实根,再用判别式求解.
解:(1)依题意,
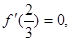
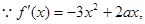
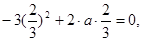
 …………………………3分
…………………………3分(2)若
 在区间(—2,3)内有两个不同的极值点,
在区间(—2,3)内有两个不同的极值点,则方程
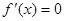 在区间(—2,3)内有两个不同的实根,
在区间(—2,3)内有两个不同的实根,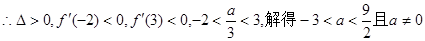
但a=0时,
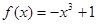 无极值点,
无极值点,∴a的取值范围为
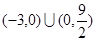
(3)在(1)的条件下,a=1,要使函数
 的图象恰有三个交点,等价于方程
的图象恰有三个交点,等价于方程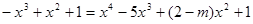 ,
,即方程
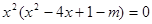 恰有三个不同的实根。
恰有三个不同的实根。 =0是一个根,
=0是一个根, 应使方程
应使方程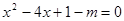 有两个非零的不等实根,
有两个非零的不等实根,由
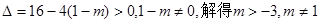
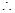 存在
存在 的图象恰有三个交点。
的图象恰有三个交点。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
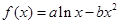 ,
,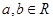 (1)若函数
(1)若函数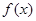 在
在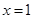 处与直线
处与直线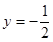 相切;
相切;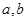 的值; ②求函数
的值; ②求函数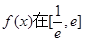 上的最大值;
上的最大值;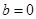 时,若不等式
时,若不等式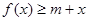 对所有的
对所有的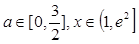 都成立,求实数
都成立,求实数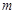 的取值范围.
的取值范围.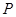 (-1,2)且与曲线
(-1,2)且与曲线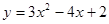 在点
在点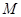 (1,1)处的切线平行的直线方程是______.
(1,1)处的切线平行的直线方程是______.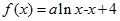 ,(
,(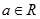 ),曲线
),曲线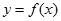 在点
在点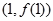 处的切线垂直于
处的切线垂直于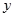 轴.
轴.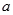 的值;
的值;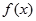 的极值。
的极值。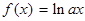 (
(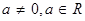 ),
),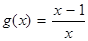 .
.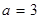 时,解关于
时,解关于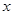 的不等式:
的不等式: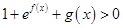 ;
;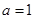 时,记
时,记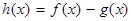 ,过点
,过点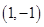 是否存在函数
是否存在函数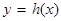 图象的切线?若存在,有多少条?若不存在,说明理由;
图象的切线?若存在,有多少条?若不存在,说明理由;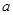 是使
是使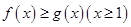 恒成立的最小值,对任意
恒成立的最小值,对任意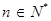 ,
,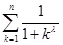 与
与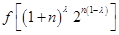 的大小(常数
的大小(常数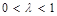 ).
).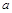 为实数,函数
为实数,函数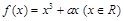 在
在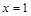 处有极值,则曲线
处有极值,则曲线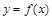 在原点处的切线方程为( )
在原点处的切线方程为( )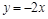
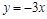
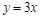
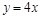
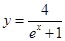 上,
上,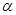 为曲线在点P处的切线的倾斜角,则
为曲线在点P处的切线的倾斜角,则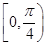
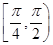
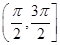
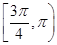
 上的函数
上的函数 满足
满足 ,且
,且 在
在 的解集为
的解集为



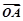 、
、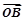 、
、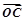 满足
满足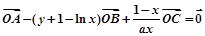 ,(O不在直线l上
,(O不在直线l上 )
) 的表达式;
的表达式; 在
在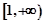 上为增函数,求a的范围;
上为增函数,求a的范围;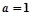 时,求证:
时,求证: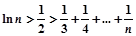 对
对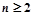 的正整数n成立.
的正整数n成立.