题目内容
14.已知f(x)=ax2+bx(a≠0),若-1≤f(-1)≤2,2≤f(1)≤4且ac2+bc-b=0(a,b,c∈R),则实数c的取值范围是[$\frac{-3-\sqrt{21}}{2}$,$\frac{-3+\sqrt{21}}{2}$].分析 由已知-1≤f(-1)≤2,2≤f(1)≤4,利用线性规划可得:a∈[$\frac{1}{2}$,3],b∈[0,$\frac{5}{2}$],$\frac{b}{a}$∈[0,3],又由ac2+bc-b=0可得:c<1,$\frac{b}{a}$(c-1)≥3(c-1),整理得:c2+3c-3≤0,解得实数c的取值范围.
解答 解:∵f(x)=ax2+bx(a≠0),若-1≤f(-1)≤2,2≤f(1)≤4
∴$\left\{\begin{array}{l}-1≤a-b≤2\\ 2≤a+b≤4\end{array}\right.$,
其对应的平面区域如下图所示: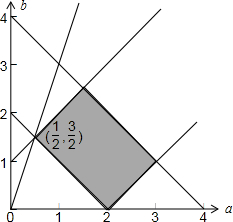
由图可知:a∈[$\frac{1}{2}$,3],b∈[0,$\frac{5}{2}$],$\frac{b}{a}$∈[0,3]
又∵且ac2+bc-b=0,则当c≥1时,ac2+bc-b≥a不成立,故c<1,
则$\frac{b}{a}$(c-1)≥3(c-1),
即c2+$\frac{b}{a}$c-$\frac{b}{a}$≥c2+3c-3,
即ac2+bc-b=0≥a(c2+3c-3)
即c2+3c-3≤0,
解得:c∈[$\frac{-3-\sqrt{21}}{2}$,$\frac{-3+\sqrt{21}}{2}$],
故答案为:[$\frac{-3-\sqrt{21}}{2}$,$\frac{-3+\sqrt{21}}{2}$]
点评 本题考查的知识点是二次函数的图象和性质,线性规划,本题转化困难,属于难题.

练习册系列答案
相关题目
4.某工厂为了调查工人文化程度与月收入的关系,随机抽取了部分工人,得到如下列表:
文化程度与月收入列联表(单位:人)
由上表中数据计算得K2=$\frac{{105×{{({10×30-20×45})}^2}}}{55×50×30×75}$≈6.109,请根据下表,估计有多大把握认为“文化程度与月收入有关系”( )
文化程度与月收入列联表(单位:人)
| 月收入2000元以下 | 月收入2000元及以上 | 总计 | |
| 高中文化以上 | 10 | 45 | 55 |
| 高中文化及以下 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| A. | 1% | B. | 99% | C. | 2.5% | D. | 97.5% |
5.y=$\frac{{x}^{2}}{x+3}$的导数是( )
| A. | $\frac{{x}^{2}-6x}{(x+3)^{2}}$ | B. | $\frac{{x}^{2}+6x}{x+3}$ | C. | $\frac{{x}^{2}}{(x+3)^{2}}$ | D. | $\frac{{x}^{2}+6x}{(x+3)^{2}}$ |
