题目内容
【题目】已知函数![]() (
(![]() 为实常数且
为实常数且![]() ).
).
(Ⅰ)当![]() 时;
时;
①设![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
②求证:函数![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅱ)设集合![]() ,若
,若![]() ,求
,求![]() 的取值范围(用
的取值范围(用![]() 表示).
表示).
【答案】(Ⅰ)①见解析,②见解析,(Ⅱ)![]()
【解析】
(Ⅰ)①确定函数的解析式,然后利用函数的定义域,及g(-x)=g(x),g判断函数的奇偶性;②利用二次函数与复合函数的单调性的,可证得函数的单调性
(Ⅱ)将原问题转化为恒成立的问题,结合恒成立的条件即可求得实数λ的范围.
(Ⅰ)①函数为偶函数,证明如下:
当a=1,b=3时,![]() ,∴g(x)=f(x+2)=
,∴g(x)=f(x+2)=![]() ,
,
其定义域为{x|x≠1且x≠-1},函数的定义域关于坐标原点对称,
g(-x)=![]() =g(x),故g(x)是偶函数.
=g(x),故g(x)是偶函数.
②![]() ,
,
令u(x)=![]() ,
,
易知u(x)在![]() 上是增函数,u(x)的值域为[-1,0), f(u)=
上是增函数,u(x)的值域为[-1,0), f(u)=![]() 在[-1,0)上增函数,故
在[-1,0)上增函数,故![]() 在
在![]() 上是增函数.
上是增函数.
(Ⅱ)因为M∩N=,所以函数y=f(x)与y=![]() 的图象无公共点,
的图象无公共点,
即方程![]() (﹡)无无实解,
(﹡)无无实解,
![]() ,
,
当λ=0时,方程无解,显然符合题意,
当λ≠0时,令y=(xa)(xb)![]() =
=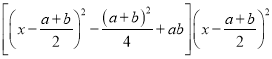 ,
,
令t=![]() ,则y=
,则y=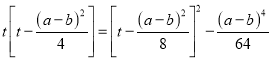 ,
,
当t=![]() 时,ymin=
时,ymin=![]() ,
,
所以,要使(﹡)无实数解,只要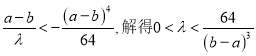 ,
,
综上,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目