ЬтФПФкШн
ЁОЬтФПЁП2019ФъЕкЪЎШ§НьХЎХХЪРНчБЙВ12жЇВЮШќЧђЖгЃЌБШШќШќжЦсШЁЕЅбЛЗЗНЪНЃЌМДУПжЇЧђЖгНјаа11ГЁБШШќЃЌзюКѓППЛ§ЗжбЁГізюКѓЙкОќЃЎЛ§ЗжЙцдђШчЯТЃЈБШШќВЩШЁ5Ож3ЪЄжЦЃЉЃКБШШќжавд3ЁЊ0Лђ3ЁЊ1ШЁЪЄЕФЧђЖгЛ§3ЗжЃЌИКЖгЛ§0ЗжЃЛЖјдкБШШќжавд3ЁЊ2ШЁЪЄЕФЧђЖгЛ§2ЗжЃЌИКЖгЛ§1ЗжЃЎ9ТжЙ§КѓЃЌЛ§ЗжАёЩЯЕФЧА2УћЗжБ№ЮЊжаЙњЖгКЭУРЙњЖгЃЌжаЙњЖгЛ§26ЗжЃЌУРЙњЖгЛ§22ЗжЃЎЕк10ТжжаЙњЖгЖдПЙШћЖћЮЌбЧЖгЃЌЩшУПОжБШШќжаЙњЖгШЁЪЄЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕк10ТжБШШќжаЃЌМЧжаЙњЖг3ЁЊ1ШЁЪЄЕФИХТЪЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюДѓжЕЕу
ЕФзюДѓжЕЕу![]() ЃЎ
ЃЎ
ЃЈ2ЃЉвдЃЈ1ЃЉжаЕФ![]() зїЮЊ
зїЮЊ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈiЃЉдкЕк10ТжБШШќжаЃЌжаЙњЖгЫљЕУЛ§ЗжЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаЃЛ
ЕФЗжВМСаЃЛ
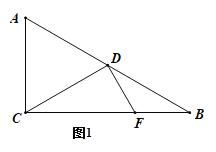
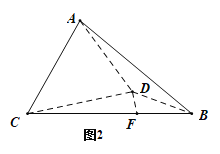
ЃЈЂЂЃЉвбжЊЕк10ТжУРЙњЖгЛ§3ЗжЃЌХаЖЯжаЙњЖгФмЗёЬсЧАвЛТжЖсЕУЙкОќЃЈЕк10ТжЙ§КѓЃЌЮоТлзюКѓвЛТжМДЕк11ТжНсЙћШчКЮЃЌжаЙњЖгЛ§ЗжзюЖрЃЉЃПШєФмЃЌЧѓГіЯргІЕФИХТЪЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉЃЈiЃЉМћНтЮіЃЈЂЂЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЕУГі![]() ЃЌНсКЯЕМЪ§ЕУГіКЏЪ§
ЃЌНсКЯЕМЪ§ЕУГіКЏЪ§![]() ЕФЕЅЕїадЃЌНјЖјЕУГі
ЕФЕЅЕїадЃЌНјЖјЕУГі![]() ЕФзюДѓжЕЕу
ЕФзюДѓжЕЕу![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЃЈiЃЉЯШЕУГі![]() ЕФПЩФмШЁжЕЃЌдйЕУГіЦфЯргІИХТЪЃЌСаГіЗжВМСаМДПЩЃЛ
ЕФПЩФмШЁжЕЃЌдйЕУГіЦфЯргІИХТЪЃЌСаГіЗжВМСаМДПЩЃЛ
ЃЈЂЂЃЉШєжаЙњЖгдкЕк10ТжБШШќжаЃЌЛёЕУ![]() Л§ЗжЃЌдђзмЛ§ЗжЮЊ
Л§ЗжЃЌдђзмЛ§ЗжЮЊ![]() ЗжЃЌМДБуУРЙњЖгЕк
ЗжЃЌМДБуУРЙњЖгЕк![]() ЖМЛёЕУ
ЖМЛёЕУ![]() ЗжЃЌдђзмЛ§ЗжЮЊ
ЗжЃЌдђзмЛ§ЗжЮЊ![]() ЗжЃЌдђжаЙњЖгПЩвдЬсЧАвЛТжЖсЕУЙкОќЃЌзюКѓгЩЃЈiЃЉЕУГіЦфИХТЪ.
ЗжЃЌдђжаЙњЖгПЩвдЬсЧАвЛТжЖсЕУЙкОќЃЌзюКѓгЩЃЈiЃЉЕУГіЦфИХТЪ.
ЃЈ1ЃЉ![]()
гЩДЫ![]()
Сю![]() ЃЌЕУ
ЃЌЕУ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() дк
дк![]() ЩЯЮЊдіКЏЪ§ЃЛ
ЩЯЮЊдіКЏЪ§ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() дк
дк![]() ЩЯЮЊМѕКЏЪ§ЃЛ
ЩЯЮЊМѕКЏЪ§ЃЛ
Ыљвд![]() ЕФзюДѓжЕЕу
ЕФзюДѓжЕЕу![]()
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊ![]()
ЃЈiЃЉ![]() ПЩШЁ
ПЩШЁ![]()
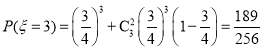


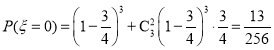
Ыљвд![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
|
|
|
|
|
|
|
|
|
|
ЃЈЂЂЃЉШє![]() ЃЌдђжаЙњЖг
ЃЌдђжаЙњЖг![]() ТжКѓЕФзмЛ§ЗжЮЊ
ТжКѓЕФзмЛ§ЗжЮЊ![]() ЗжЃЌУРЙњЖгМДБуЕк
ЗжЃЌУРЙњЖгМДБуЕк![]() ТжКЭЕк
ТжКЭЕк![]() ТжЖМЛ§
ТжЖМЛ§![]() ЗжЃЌдђ
ЗжЃЌдђ![]() ТжЙ§КѓЕФзмЛ§ЗжЪЧ
ТжЙ§КѓЕФзмЛ§ЗжЪЧ![]() ЗжЃЌ
ЗжЃЌ![]() ЃЌЫљвдЃЌжаЙњЖгШчЙћЕк
ЃЌЫљвдЃЌжаЙњЖгШчЙћЕк![]() ТжЛ§
ТжЛ§![]() ЗжЃЌдђПЩЬсЧАвЛТжЖсЕУЙкОќЃЌЦфИХТЪЮЊ
ЗжЃЌдђПЩЬсЧАвЛТжЖсЕУЙкОќЃЌЦфИХТЪЮЊ![]()

ЁОЬтФПЁПНќФъРДЃЌЙВЯэЕЅГЕдкЮвЙњИїГЧЪабИУЭЗЂеЙЃЌЮЊШЫУЧЕФГіааЬсЙЉСЫБуРћЃЌЕЋвВИјГЧЪаЕФНЛЭЈЙмРэДјРДСЫвЛаЉРЇФбЃЌЮЊеЦЮеЙВЯэЕЅГЕдк![]() ЪЁЕФЗЂеЙЧщПіЃЌФГЕїВщЛњЙЙДгИУЪЁГщШЁСЫ5ИіГЧЪаЃЌВЂЭГМЦСЫЙВЯэЕЅГЕЕФ
ЪЁЕФЗЂеЙЧщПіЃЌФГЕїВщЛњЙЙДгИУЪЁГщШЁСЫ5ИіГЧЪаЃЌВЂЭГМЦСЫЙВЯэЕЅГЕЕФ![]() жИБъ
жИБъ![]() КЭ
КЭ![]() жИБъ
жИБъ![]() ЃЌЪ§ОнШчЯТБэЫљЪОЃК
ЃЌЪ§ОнШчЯТБэЫљЪОЃК
ГЧЪа1 | ГЧЪа2 | ГЧЪа3 | ГЧЪа4 | ГЧЪа5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
ЃЈ1ЃЉЪдЧѓ![]() гы
гы![]() МфЕФЯрЙиЯЕЪ§
МфЕФЯрЙиЯЕЪ§![]() ЃЌВЂЫЕУї
ЃЌВЂЫЕУї![]() гы
гы![]() ЪЧЗёОпгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЈШє
ЪЧЗёОпгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЈШє![]() ЃЌдђШЯЮЊ
ЃЌдђШЯЮЊ![]() гы
гы![]() ОпгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЌЗёдђШЯЮЊУЛгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЉ.
ОпгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЌЗёдђШЯЮЊУЛгаНЯЧПЕФЯпадЯрЙиЙиЯЕЃЉ.
ЃЈ2ЃЉНЈСЂ![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬЃЌВЂдЄВтЕБ
ЕФЛиЙщЗНГЬЃЌВЂдЄВтЕБ![]() жИБъЮЊ7ЪБЃЌ
жИБъЮЊ7ЪБЃЌ![]() жИБъЕФЙРМЦжЕ.
жИБъЕФЙРМЦжЕ.
ЃЈ3ЃЉШєФГГЧЪаЕФЙВЯэЕЅГЕ![]() жИБъ
жИБъ![]() дкЧјМф
дкЧјМф![]() ЕФгвВрЃЌдђШЯЮЊИУГЧЪаЙВЯэЕЅГЕЪ§СПЙ§ЖрЃЌЖдГЧЪаЕФНЛЭЈЙмРэгаНЯДѓЕФгАЯьНЛЭЈЙмРэВПУХНЋНјаажЮРэЃЌжБжС
ЕФгвВрЃЌдђШЯЮЊИУГЧЪаЙВЯэЕЅГЕЪ§СПЙ§ЖрЃЌЖдГЧЪаЕФНЛЭЈЙмРэгаНЯДѓЕФгАЯьНЛЭЈЙмРэВПУХНЋНјаажЮРэЃЌжБжС![]() жИБъ
жИБъ![]() дкЧјМф
дкЧјМф![]() ФкЯжвбжЊ
ФкЯжвбжЊ![]() ЪЁФГГЧЪаЙВЯэЕЅГЕЕФ
ЪЁФГГЧЪаЙВЯэЕЅГЕЕФ![]() жИБъЮЊ13ЃЌдђИУГЧЪаЕФНЛЭЈЙмРэВПУХЪЧЗёашвЊНјаажЮРэЃПЪдЫЕУїРэгЩ.
жИБъЮЊ13ЃЌдђИУГЧЪаЕФНЛЭЈЙмРэВПУХЪЧЗёашвЊНјаажЮРэЃПЪдЫЕУїРэгЩ.
ВЮПМЙЋЪНЃКЛиЙщжБЯп![]() жааБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
жааБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
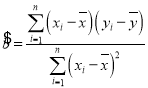 ЃЌЃЌ
ЃЌЃЌ![]() ЯрЙиЯЕЪ§
ЯрЙиЯЕЪ§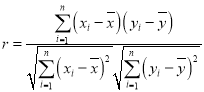
ВЮПМЪ§ОнЃК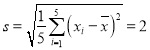 ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.