��Ŀ����
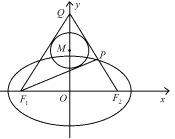
����Ŀ����֪F(0,1)Ϊƽ����һ�㣬HΪֱ��l��y=��1������һ�㣬����H��ֱ��l�Ĵ���m�����߶�FH���д�����ֱ��m���ڵ�P���ǵ�P�Ĺ켣Ϊ��.
��1����켣���ķ��̣�
��2������F�����ഹֱ��ֱ��AB��CD������ֱ��AB��켣�����ڵ�AB��ֱ��CD��켣�����ڵ�CD�����M��N�ֱ���AB��CD���е�.
����ֱ��MN�Ƿ������㣬����������㣬����ö��㣬����˵�����ɣ�
�����FMN���������Сֵ.
���𰸡���1��![]() .��2���ٺ�����㣬����Ϊ(0��3)��4
.��2���ٺ�����㣬����Ϊ(0��3)��4
��������
��1����P�����꣬������ɵ�|PF|=|PH|�������ɵ�P�Ĺ켣���̣�
��2����������ɵ�ֱ��BA��CD��б�ʶ����ڣ���ֱ��AB�ķ����������������������֮�ͣ��������AB���е�M�����꣬ͬ���ɵ�N�����꣬�������ֱ��MN��б�ʣ�����ֱ��MN�ķ��̣��ɵú�����㣻
����Ϊֱ��MN������㣬���Ե�S��FMN![]() |xM��xN|���ɾ�ֵ����ʽ�ɵá�FMN���������СֵΪ4.
|xM��xN|���ɾ�ֵ����ʽ�ɵá�FMN���������СֵΪ4.
��1����P������(x��y)������ɵ�|PF|=|PH|��
����![]() |y+1|��
|y+1|��
�����ɵ�x2=4y��
���Թ켣���ķ��̣�x2=4y��
��2��������ɵ�ֱ��AB��CD��б�ʾ����ڣ���ֱ��AB�ķ��̣�y=kx+1��A(x1��y1)��B(x2��y2)��
ֱ��������������![]() �������ɵã�x2��4kx��4=0��x1+x2=4k��y1+y2=k(x1+x2)+2=4k2+2��
�������ɵã�x2��4kx��4=0��x1+x2=4k��y1+y2=k(x1+x2)+2=4k2+2��
����AB���е�M(2k��2k2+1)��
ͬ���ɵ�N(![]() 1)��
1)��
����ֱ��MN��б��Ϊ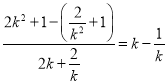 ��
��
����ֱ��MN�ķ���Ϊ��y��(2k2+1)=(k![]() )(x��2k)��
)(x��2k)��
�����ɵ�y=(k![]() )x+3�����Ժ������Q(0��3).
)x+3�����Ժ������Q(0��3).
������ֱ�ߺ������(0��3)��
�ڴӶ��ɵ�S��FMN![]() |xM��xN|
|xM��xN|![]() |2k
|2k![]() |=2|k
|=2|k![]() |��4����
|��4����![]() ʱȡ�õȺ�.
ʱȡ�õȺ�.
���ԡ�FMN���������СֵΪ4.


����Ŀ��Ϊ����ǿѧ���Ļ�����ʶ��ij��ѧ�����ȡ��50��ѧ��������һ�λ���֪ʶ���������ξ����ijɼ����÷־�Ϊ����������100�֣��������Ƴ��±���
�ɼ� |
|
|
|
|
|
|
Ƶ�� | 2 | 3 | 14 | 15 | 14 | 4 |
��1�����������ѧ���ɼ���Ƶ�ʷֲ�ֱ��ͼ��
��2�����ӳɼ���![]() ��ѡһ��ѧ�����ӳɼ���
��ѡһ��ѧ�����ӳɼ���![]() ��ѡ��2��ѧ������3��ѧ���ٿ���̸�ᣬ��
��ѡ��2��ѧ������3��ѧ���ٿ���̸�ᣬ��![]() ����ѧ��
����ѧ��![]() ��
��![]() ����ѧ��
����ѧ��![]() ͬʱ��ѡ�еĸ��ʣ�
ͬʱ��ѡ�еĸ��ʣ�