题目内容
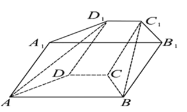
【题目】如图，在四棱柱
中，底面
是等腰梯形，
，顶点
在底面内的射影恰为点
．
（1）求证：
平面
；
（2）若直线
与底面所成的角为
，求平面
与平面所成锐二面角的余弦值．
【答案】（1）见解析（2）
【解析】
（1）如图，连接
，证明
和
，
平面
即得证；
（2）以
为坐标原点，分别以
所在直线为
轴，
轴，
轴，建立如图所示的空间直角坐标系， 利用向量法求出平面
与平面所成锐二面角的余弦值．
（1）证明：
如图，连接，则
平面
，
因为
平面
，
在等腰梯形中，连接，过点作
于点
，
，
则
因此满足
又
面
所以
平面 .
（2）
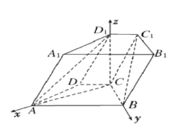
由（1）知
两两垂直，
平面
以为坐标原点，分别以所在直线为轴，轴，轴，建立如图所示的空间直角坐标系，
则
设平面的法向量
，由
得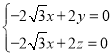
可得平面的一个法向量
平面的一个法向量
，
设平面与平面所成锐二面角为
则
.
因此平面
与平面所成锐二面角的余弦值为．
举一反三期末百分冲刺卷系列答案
【题目】为了增强学生的环境意识，某中学随机抽取了50名学生举行了一次环保知识竞赛，本次竞赛的成绩（得分均为整数，满分100分）整理，制成下表：
成绩 |
|
|
|
|
|
|
频数 | 2 | 3 | 14 | 15 | 14 | 4 |
（1）作出被抽查学生成绩的频率分布直方图；
（2）若从成绩在
中选一名学生，从成绩在
中选出2名学生，共3名学生召开座谈会，求组中学生
和组中学生
同时被选中的概率？
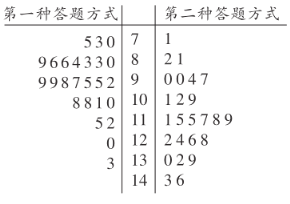
【题目】某市实验中学数学教研组，在高三理科一班进行了一次“采用两种不同方式进行答卷”的考试实验，第一种做卷方式：按从前往后的顺序依次做；第二种做卷方式：先做简单题，再做难题.为了比较这两种做卷方式的效率，选取了
名学生，将他们随机分成两组，每组
人.第一组学生用第一种方式，第二组学生用第二种方式，根据学生的考试分数（单位：分）绘制了茎叶图如图所示.
若
分（含分）以上为优秀，根据茎叶图估计两种做卷方式的优秀率；
设名学生考试分数的中位数为
，根据茎叶图填写下面的
列联表：
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 | |||
第一种做卷方式 | |||
合计 |
根据列联表，能否有
的把握认为两种做卷方式的效率有差异？
附：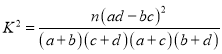
，
.
|
|
|
|
|
|
|
|
