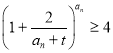题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 的零点个数;
的零点个数;
(Ⅱ)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 的零点个数为1;(Ⅱ)
的零点个数为1;(Ⅱ)![]()
【解析】
(Ⅰ)根据题意,代入![]() ,对函数求导,判断函数单调性,根据特殊值
,对函数求导,判断函数单调性,根据特殊值![]() ,即可判断零点个数;
,即可判断零点个数;
(Ⅱ)根据题意,解决函数![]() 恒成立问题,方法一:转化
恒成立问题,方法一:转化![]() 对任意
对任意![]() 恒成立,则有
恒成立,则有![]() 对任意
对任意![]() 恒成立,构造函数
恒成立,构造函数![]() ,只需求
,只需求![]() ,利用导数研究函数最值问题。方法二:
,利用导数研究函数最值问题。方法二:![]() 对任意
对任意![]() 恒成立.构造函数
恒成立.构造函数![]() ,转化成射线
,转化成射线![]() 与函数
与函数![]() 的图象相切时属临界状态,计算求解;方法三:含参的函数最小值探究,只需
的图象相切时属临界状态,计算求解;方法三:含参的函数最小值探究,只需![]() ,即可求解参数取值范围.
,即可求解参数取值范围.
(Ⅰ)当![]() 时,
时,![]() ,其定义域为
,其定义域为![]() ,
,
求导得![]() ,
,
于是当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,又
单调递增,又![]() ,所以函数
,所以函数![]() 的零点个数为1;
的零点个数为1;
(Ⅱ)法1:因对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,于是
恒成立,于是![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,只需
,只需![]() .
.
对函数![]() 求导,得
求导,得![]() ,令
,令![]() ,
,
则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递增,所以函数
单调递增,所以函数![]() ,于是
,于是![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() .
.
法2:因对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立.构造函数
恒成立.构造函数![]() ,对其求导,得
,对其求导,得![]() ,
,
令![]() ,得
,得![]() (
(![]() 舍去),所以当
舍去),所以当 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当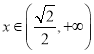 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
函数![]() 的图象是一条过原点的射线(不包括端点),旋转射线(不含端点),发现
的图象是一条过原点的射线(不包括端点),旋转射线(不含端点),发现![]() 与函数
与函数![]() 的图象相切时属临界状态.
的图象相切时属临界状态.
设切点为![]() ,则
,则![]() ,整理得
,整理得![]() ,
,
显然![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,所以
,所以![]() ,此时切线斜率为1,结合图象,可知实数
,此时切线斜率为1,结合图象,可知实数![]() 的取值范围为
的取值范围为![]() .
.
法3:根据题意只需![]() 即可.
即可.
又![]() ,令
,令![]() ,因2与
,因2与![]() 异号,所以必有一正根,不妨设为
异号,所以必有一正根,不妨设为![]() ,则
,则![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,所以
单调递增,所以![]() ,
,
又![]() 在
在![]() 上是减函数,又
上是减函数,又![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() 在
在![]() 上单调递增,则实数
上单调递增,则实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目