题目内容
已知函数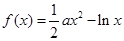 ,
,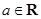 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 在区间
在区间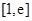 的最小值为
的最小值为 ,求
,求 的值.
的值.
(1)当 时,函数
时,函数 的单调减区间是
的单调减区间是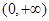 ,当
,当 时,函数
时,函数 的单调减区间是
的单调减区间是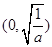 ,单调增区间为
,单调增区间为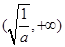 ;(2)
;(2) .
.
解析试题分析:(1)求函数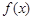 的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数
的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数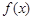 的单调区间,求函数
的单调区间,求函数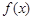 导函数
导函数 ,令
,令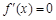 ,找出分界点,从而确定函数的单调区间,但由于含有参数
,找出分界点,从而确定函数的单调区间,但由于含有参数 ,需对参数
,需对参数 分
分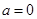 ,
, ,
, 讨论,从而得函数
讨论,从而得函数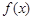 的单调区间;(2)若函数
的单调区间;(2)若函数 在区间
在区间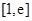 的最小值为
的最小值为 ,求
,求 的值,求出函数
的值,求出函数 在区间
在区间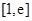 的最小值,令它等于为
的最小值,令它等于为 即可,由(1)可知,当
即可,由(1)可知,当 时,函数
时,函数 的单调减区间是
的单调减区间是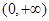 ,
, 的最小值为
的最小值为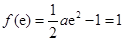 ,解出
,解出 ,验证是否符合,当
,验证是否符合,当 时,函数
时,函数 的单调减区间是
的单调减区间是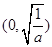 ,单调增区间为
,单调增区间为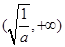 ,由于不知函数
,由于不知函数 在区间
在区间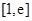 的单调性,需讨论
的单调性,需讨论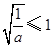 ,
, ,
,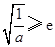 ,分别求出函数
,分别求出函数 在区间
在区间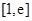 的最小值,令它等于为
的最小值,令它等于为 ,解出
,解出 ,验证是否符合,从而得
,验证是否符合,从而得 的值.
的值.
试题解析:函数 的定义域是
的定义域是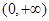 ,
, 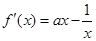
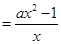 .
.
(1)(1)当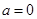 时,
时,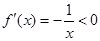 ,故函数
,故函数 在
在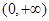 上单调递减.
上单调递减.
(2)当 时,
时,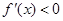 恒成立,所以函数
恒成立,所以函数 在
在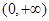 上单调递减.
上单调递减.
(3)当 时,令
时,令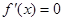 ,又因为
,又因为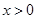 ,解得
,解得 .
.
①当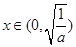 时,
时,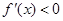 ,所以函数
,所以函数 在
在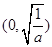 单调递减.
单调递减.
②当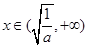 时,
时,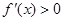 ,所以函数
,所以函数 在
在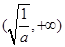 单调递增.
单调递增.
综上所述,当 时,函数
时,函数 的单调减区间是
的单调减区间是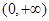 ,
,
当 时,函数
时,函数 的单调减区间是
的单调减区间是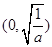 ,单调增区间为
,单调增区间为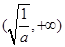 . 7分
. 7分
(2)(1)当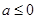 时,由(1)可知,
时,由(1)可知, 在
在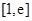 上单调递减,
上单调递减,
所以 的最小值为
的最小值为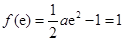 ,解得
,解得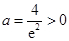 ,舍去.
,舍去.
(2)当

练习册系列答案
相关题目
 (元)表示为速度
(元)表示为速度 (海里/小时)的函数;
(海里/小时)的函数; 是自然对数的底数,函数
是自然对数的底数,函数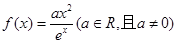 .
. 的单调递增区间;
的单调递增区间;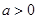 时,函数
时,函数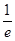 ,求
,求 的值.
的值.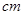 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料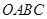 ,其中点
,其中点 在圆弧上,点
在圆弧上,点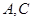 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以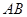 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设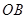 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为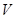
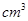 .
.
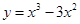 .
.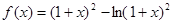 ,
,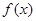 的单调区间;
的单调区间;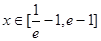 时,不等式
时,不等式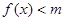 恒成立,求实数
恒成立,求实数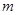 的取值范围;
的取值范围; 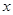 的方程
的方程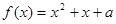 在区间
在区间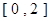 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数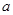 的取值范围.
的取值范围.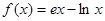 ,
, 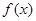 的单调区间;
的单调区间;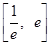 内存在
内存在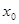 ,使不等式
,使不等式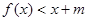 成立,求
成立,求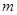 的取值范围.
的取值范围. (如图所示,其中O为圆心,
(如图所示,其中O为圆心, 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).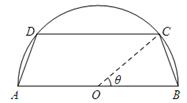
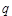 的值,使体积V最大;
的值,使体积V最大;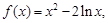
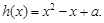
 的极值;
的极值;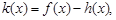 若函数
若函数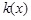 在
在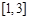 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数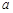 的取值范围.
的取值范围.