题目内容
某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其他费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其余费用为每小时1250元。
(1)把全程运输成本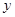 (元)表示为速度
(元)表示为速度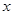 (海里/小时)的函数;
(海里/小时)的函数;
(2)为使全程运输成本最小,轮船应以多大速度行驶?
(1)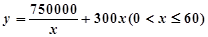 ;(2)轮船应以50海里/小时的速度行驶.
;(2)轮船应以50海里/小时的速度行驶.
解析试题分析:(1)由题意易列出速度与成本的函数;(2)由列出的函数利用导数求最值.(也可用均值不等式)
试题解析:
解:(1)由题意得: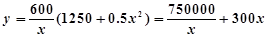 ,
,
即: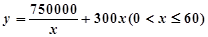 6分
6分
(2)由(1)知,
令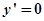 ,解得x=50,或x=-50(舍去). 8分
,解得x=50,或x=-50(舍去). 8分
当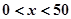 时,
时,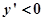
当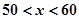 时,
时,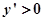 (均值不等式法同样给分) 10分
(均值不等式法同样给分) 10分
因此,函数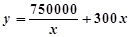 在x=50处取得极小值,也是最小值.
在x=50处取得极小值,也是最小值.
故为使全程运输成本最小,轮船应以50海里/小时的速度行驶. 12分
考点:导数的应用.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 ,
,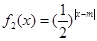 ,其中m∈R.
,其中m∈R.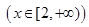 的单调性,并证明你的结论;
的单调性,并证明你的结论;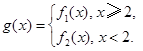 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.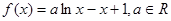 .
. 的单调区间;
的单调区间;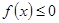 在
在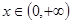 上恒成立,求所有实数
上恒成立,求所有实数 的值;
的值;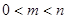 ,证明:
,证明: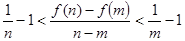
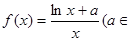 R).
R).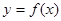 在点
在点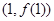 处的切线与直线
处的切线与直线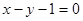 平行,求
平行,求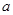 的值;
的值; 的单调区间和极值;
的单调区间和极值; ,且
,且 时,证明:
时,证明:
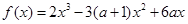
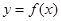 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;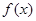 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值.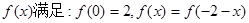 ,它的导函数的图象与直线
,它的导函数的图象与直线 平行.
平行. 的解析式;
的解析式; 的图象与直线
的图象与直线 有三个公共点,求m的取值范围.
有三个公共点,求m的取值范围.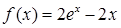 ,
,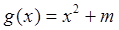 (
(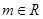 ).
). 的单调性;
的单调性;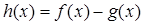 ,
,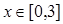 ,当函数
,当函数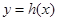 有零点时,求实数
有零点时,求实数 的最大值.
的最大值.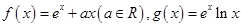 (e为自然对数的底数).
(e为自然对数的底数).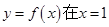 处的切线为
处的切线为 ,若
,若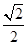 ,求a的值;
,求a的值;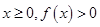 恒成立,试确定
恒成立,试确定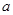 的取值范围;
的取值范围;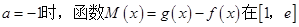 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.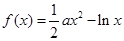 ,
,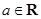 .
. 的单调区间;
的单调区间;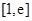 的最小值为
的最小值为 ,求
,求 的值.
的值.