题目内容
已知函数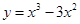 .
.
(1)求函数的极小值;
(2)求函数的递增区间.
(1)极小值为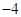 ;(2)函数的单调递增区间为
;(2)函数的单调递增区间为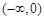 ,
,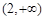 .
.
解析试题分析:(1)先确定函数的定义域并求出函数的导数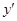 ,然后确定
,然后确定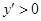 、
、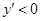 的
的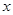 的取值范围,最后根据可导函数的极小值点的左侧导数小于0,右侧大于0,从而确定函数的极小值;(2)由
的取值范围,最后根据可导函数的极小值点的左侧导数小于0,右侧大于0,从而确定函数的极小值;(2)由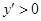 ,即可求出函数的单调递增区间.
,即可求出函数的单调递增区间.
试题解析:(1) ∵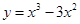 ∴
∴ 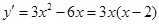 3分
3分
所以当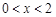 时,
时,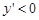 ;当
;当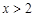 或
或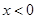 时,
时,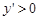 6分
6分
∴ 当 时,函数有极小值
时,函数有极小值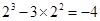 8分
8分
(2)由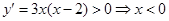 或
或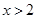 11分
11分
∴ 函数的递增区间是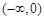 ,
,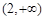 12分.
12分.
考点:1.函数的极值与导数;2.函数的单调性与导数.

练习册系列答案
相关题目
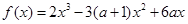
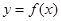 在点(2,f (2))处的切线方程;
在点(2,f (2))处的切线方程;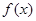 在闭区间[0,|2a|]上的最小值.
在闭区间[0,|2a|]上的最小值. (如图所示,其中O为圆心,
(如图所示,其中O为圆心, 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).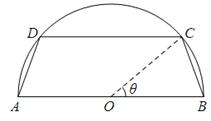
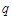 的值,使体积V最大;
的值,使体积V最大;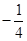 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;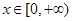 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在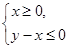 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;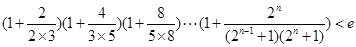 (其中
(其中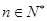 ,e是自然数对数的底数)
,e是自然数对数的底数) 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?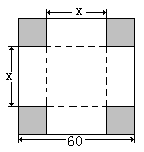
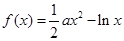 ,
,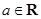 .
. 的单调区间;
的单调区间;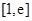 的最小值为
的最小值为 ,求
,求 的值.
的值.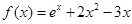 .
. 在区间
在区间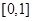 上存在唯一的极值点;
上存在唯一的极值点;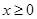 时,若关于
时,若关于 的不等式
的不等式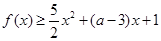 恒成立,试求实数
恒成立,试求实数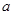 的取值范围.
的取值范围. 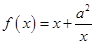 ,
,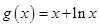 ,其中
,其中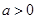 .
.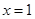 是函数
是函数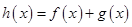 的极值点,求实数
的极值点,求实数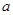 的值;
的值;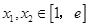 (
(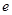 为自然对数的底数)都有
为自然对数的底数)都有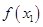 ≥
≥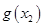 成立,求实数
成立,求实数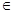 R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.
R),使得f(x)≥kx十b且g(x)≤kx+b对一切x>0恒成立?若存在,求出该一次函数的表达式;若不存在,请说明理由.