题目内容
【题目】已知点![]() 是椭圆
是椭圆![]() 上任一点,点
上任一点,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,到点
,到点![]() 的距离为
的距离为![]() ,且
,且![]() .直线
.直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 为椭圆与
为椭圆与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 方程;
方程;
(3)对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.

【答案】(1) ![]() (2)
(2) ![]() (3)直线
(3)直线![]() 总经过定点
总经过定点![]()
【解析】试题分析:(1) 设![]() ,用坐标表示条件
,用坐标表示条件![]() 列出方程化简整理可得椭圆的标准方程;(2)由(1)可知
列出方程化简整理可得椭圆的标准方程;(2)由(1)可知![]() ,
, ![]() ,即可得
,即可得![]() ,由
,由![]() 得
得![]() ,写出直线
,写出直线![]() 的方程与椭圆方程联立,求出点
的方程与椭圆方程联立,求出点![]() 的坐标,由两点式求直线
的坐标,由两点式求直线![]() 的方程即可;(3)由
的方程即可;(3)由![]() ,得
,得![]() ,设直线
,设直线![]() 方程为
方程为![]() ,与椭圆方程联立得
,与椭圆方程联立得![]() ,由根与系数关系计算
,由根与系数关系计算![]() 得
得![]() ,从而得到直线方程为
,从而得到直线方程为![]() ,从而得到直线过定点
,从而得到直线过定点![]() .
.
试题解析: (1)设![]() ,则
,则![]() ,
, ![]() ,………………1分
,………………1分
∴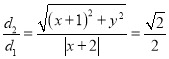 ,化简,得
,化简,得![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .………………3分
.………………3分
(2)![]() ,
, ![]() ,∴
,∴![]() ,………………4分
,………………4分
又∵![]() ,∴
,∴![]() ,
, ![]() .
.
代入![]() 解,得
解,得![]() (舍)
(舍)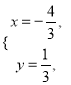 ∴
∴![]() ,………………6分
,………………6分
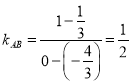 ,∴
,∴![]() .即直线
.即直线![]() 方程为
方程为![]() .………………7分
.………………7分
(3)∵![]() ,∴
,∴![]() .
.
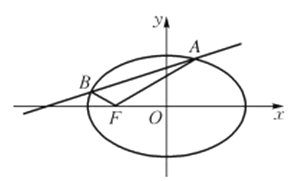
设![]() ,
,![]() ,直线
,直线![]() 方程为
方程为![]() .代直线
.代直线![]() 方程
方程![]() 入
入![]() ,得
,得
![]() .………………9分
.………………9分
∴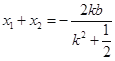 ,
,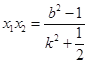 ,∴
,∴![]() =
=
![]() ,
,
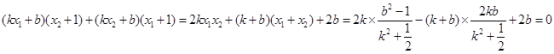 ∴
∴![]() ,……………11分
,……………11分
∴直线![]() 方程为
方程为![]() ,
,
∴直线![]() 总经过定点
总经过定点![]() .………………12分
.………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
