题目内容
【题目】设
为一个56元集合.求最小的正整数
，使得对集合的任意15个子集，只要它们中间任何七个的并的元素个数均不少于，则这15个子集中一定存在三个集合，使得它们的交集非空.
【答案】41
【解析】
构造15个子集
，
.
则
，
，
，
.
于是，这15个子集中任何三个中必有两个是
组，或者必有两个是
组，三者交集均为空集.
现分析其中任何七个子集的元素个数.
任取其中七个子集
，
，…，
及
，
，…，
，其中，
.则
.
故满足题设的正整数
.
下面用反证法证明：
满足题设.
假设存在集合
的某15个子集
，
，…，
.尽管其中任何七个子集的并集不少于41个元素，但其中任何三个子集的交集均为空集，从而，每个元素至多属于两个子集.
分两种情形讨论.
（1）集合的每个元素均恰属于，，…，中两个子集.
由抽屉原理，知必有一个子集（不妨设为）中至少含有
（
表示不超过实数
的最大整数）个元素.由，，…，
组成的所有七元子集组，至少共对应
个元素.
另一方面，对任一元素
，若
，则，，…，中只有两个子集含有，于是，被计算的次数为
；若
，则，，…，中只有一个子集含有，于是，被计算的次数为
.
故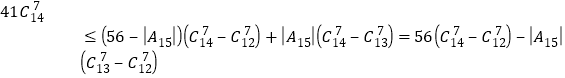
，即
，矛盾.
（2）集合可能存在一些元素至多属于子集，，…，中一个子集.
在不含这些元素的子集中各找一个添入这些元素，直至集合的每个元素均恰含于子集，，…，中两个子集.于是，改造过的子集，，…，中的任意三个的交仍然为空集.此时，该情形已化为（1），从而，也是矛盾的.
总之，对于集合的任意15个子集，只要它们中任何七个的并的元素个数均不少于41，则这15个子集中就一定存在三个交集非空的集合.
综上，满足题设的最小正整数.
【题目】某学校为倡导全体学生为特困学生捐款，举行“一元钱，一片心，诚信用水”活动，学生在购水处每领取一瓶矿泉水，便自觉向捐款箱中至少投入一元钱。现统计了连续5天的售出和收益情况，如下表：
售出水量x（单位：箱） | 7 | 6 | 6 | 5 | 6 |
收益y（单位：元） | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x与y成线性相关，则某天售出8箱水时，预计收益为多少元？
(Ⅱ) 期中考试以后，学校决定将诚信用水的收益，以奖学金的形式奖励给品学兼优的特困生，规定：特困生考入年级前200名，获一等奖学金500元；考入年级201—500 名，获二等奖学金300元；考入年级501名以后的特困生将不获得奖学金。甲、乙两名学生获一等奖学金的概率均为
，获二等奖学金的概率均为
，不获得奖学金的概率均为
.
⑴在学生甲获得奖学金条件下，求他获得一等奖学金的概率；
⑵已知甲、乙两名学生获得哪个等第的奖学金是相互独立的，求甲、乙两名学生所获得奖学金总金额X 的分布列及数学期望。
附：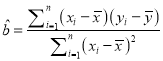 
， 
。
