题目内容
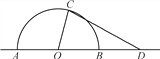
【题目】如图,△ABC中,sin ![]() =
= ![]() ,AB=2,点D在线段AC上,且AD=2DC,BD=
,AB=2,点D在线段AC上,且AD=2DC,BD= ![]() .(Ⅰ)求:BC的长;(Ⅱ)求△DBC的面积.
.(Ⅰ)求:BC的长;(Ⅱ)求△DBC的面积. 
【答案】解:(Ⅰ)因为sin ![]() =
= ![]() ,所以cos∠ABC=1﹣2
,所以cos∠ABC=1﹣2 ![]() =1﹣2×
=1﹣2× ![]() =
= ![]() . 在△ABC中,设BC=a,AC=3b,
. 在△ABC中,设BC=a,AC=3b,
由余弦定理可得: ![]() ①
①
在△ABD和△DBC中,由余弦定理可得: ,
, 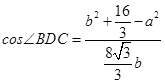 .
.
因为cos∠ADB=﹣cos∠BDC,所以有  ,所以3b2﹣a2=﹣6 ②
,所以3b2﹣a2=﹣6 ②
由①②可得a=3,b=1,即BC=3.
(Ⅱ)由(Ⅰ)知cos∠ABC= ![]() ,则sin∠ABC=
,则sin∠ABC= 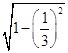 =
= ![]() ,又AB=2,BC=3,
,又AB=2,BC=3,
则△ABC的面积为 ![]() ABBCsin∠ABC=
ABBCsin∠ABC= ![]() ,
,
又因为AD=2DC,所以△DBC的面积为 ![]() ×2
×2 ![]() =
= ![]()
【解析】(Ⅰ)由sin ![]() 的值,利用二倍角的余弦函数公式即可求出cos∠ABC的值,设BC=a,AC=3b,由AD=2DC得到AD=2b,DC=b,在三角形ABC中,利用余弦定理得到关于a与b的关系式,记作①,在三角形ABD和三角形DBC中,利用余弦定理分别表示出cos∠ADB和cos∠BDC,由于两角互补,得到cos∠ADB等于﹣cos∠BDC,两个关系式互为相反数,得到a与b的另一个关系式,记作②,①②联立即可求出a与b的值,即可得到BC的值;(Ⅱ)由角ABC的范围和cos∠ABC的值,利用同角三角函数间的基本关系求出sin∠ABC的值,由AB和BC的值,利用三角形的面积公式即可求出三角形ABC的面积,由AD=2DC,且三角形ABD和三角形BDC的高相等,得到三角形BDC的面积等于三角形ABC面积的
的值,利用二倍角的余弦函数公式即可求出cos∠ABC的值,设BC=a,AC=3b,由AD=2DC得到AD=2b,DC=b,在三角形ABC中,利用余弦定理得到关于a与b的关系式,记作①,在三角形ABD和三角形DBC中,利用余弦定理分别表示出cos∠ADB和cos∠BDC,由于两角互补,得到cos∠ADB等于﹣cos∠BDC,两个关系式互为相反数,得到a与b的另一个关系式,记作②,①②联立即可求出a与b的值,即可得到BC的值;(Ⅱ)由角ABC的范围和cos∠ABC的值,利用同角三角函数间的基本关系求出sin∠ABC的值,由AB和BC的值,利用三角形的面积公式即可求出三角形ABC的面积,由AD=2DC,且三角形ABD和三角形BDC的高相等,得到三角形BDC的面积等于三角形ABC面积的 ![]() ,进而求出三角形BDC的面积.
,进而求出三角形BDC的面积.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案【题目】电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性. 附:K2= ![]()
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
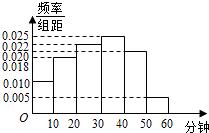
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
总计 |
(2)将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”中有2名女性,若从“超级体育迷”中任意选取2名,求至少有1名女性观众的概率.
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
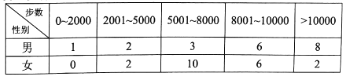
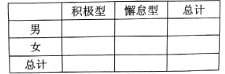
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 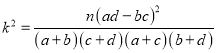 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.