题目内容
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为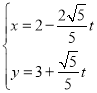 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且
上的点,且![]() .求
.求![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)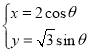 (
(![]() 为参数),
为参数),![]() ;(Ⅱ)
;(Ⅱ)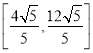 .
.
【解析】
(Ⅰ)先利用极坐标方程与直角坐标方程互化公式,把曲线![]() 的极坐标方程化成直角坐标方程,然后再判断曲线
的极坐标方程化成直角坐标方程,然后再判断曲线![]() 的类型,写出它的参数方程;利用代入消元法把直线
的类型,写出它的参数方程;利用代入消元法把直线![]() 的参数方程化为普通方程即可.
的参数方程化为普通方程即可.
(Ⅱ)根据曲线![]() 的参数方程设出点
的参数方程设出点![]() 的坐标,然后结合点到直线的距离公式、三角形面积公式、辅助角公式进行求解即可.
的坐标,然后结合点到直线的距离公式、三角形面积公式、辅助角公式进行求解即可.
(Ⅰ)由题意:![]()
![]()
![]()
![]() ,该曲线为椭圆,
,该曲线为椭圆,
![]() 曲线
曲线![]() 的参数方程为
的参数方程为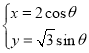 (
(![]() 为参数).
为参数).
由直线![]() 的参数方程得
的参数方程得![]() 代入
代入![]()
得![]() ,
,![]()
![]() 直线
直线![]() 的普通方程为
的普通方程为![]() .
.
(Ⅱ)设![]() 到直线
到直线![]() 的距离为
的距离为![]()
![]()
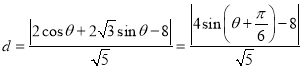
![]()
![]() 面积的取值范围是
面积的取值范围是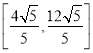 .
.

练习册系列答案
相关题目