题目内容
【题目】已知函数![]() ,
,
(1)讨论![]() 在
在![]() 上的单调性.
上的单调性.
(2)当![]() 时,若
时,若![]() 在
在![]() 上的最大值为
上的最大值为![]() ,讨论:函数
,讨论:函数![]() 在
在![]() 内的零点个数.
内的零点个数.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减;(2)
上单调递减;(2)![]() 个零点
个零点
【解析】
(1)求得![]() ,根据
,根据![]() 范围可知
范围可知![]() ,进而通过对
,进而通过对![]() 的正负的讨论得到函数单调性;
的正负的讨论得到函数单调性;
(2)由(1)可得函数在![]() 上的单调性,进而利用最大值构造方程求得
上的单调性,进而利用最大值构造方程求得![]() ,得到函数解析式;利用单调性和零点存在定理可确定
,得到函数解析式;利用单调性和零点存在定理可确定![]() 在
在![]() 上有
上有![]() 个零点;令
个零点;令![]() ,求导后,可确定
,求导后,可确定![]() 在
在![]() 上存在零点,从而得到
上存在零点,从而得到![]() 的单调性,通过单调性和零点存在定理可确定零点个数.
的单调性,通过单调性和零点存在定理可确定零点个数.
(1)![]()
当![]() 时,
时,![]()
![]() 当
当![]() ,
,![]() 时,
时,![]() ;当
;当![]() ,
,![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减
上单调递减
(2)由(1)知,当![]() 时,
时,![]() 在
在![]() 上单调递增
上单调递增
![]() ,解得:
,解得:![]()
![]()
![]()
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]()
![]() 在
在![]() 内有且仅有
内有且仅有![]() 个零点
个零点
令![]() ,
,![]()
![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]()
![]() 在
在![]() 内单调递减
内单调递减
又![]() ,
,![]()
![]() ,使得
,使得![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
![]()
![]() 在
在![]() 上无零点且
上无零点且![]()
又![]()
![]() 在
在![]() 上有且仅有
上有且仅有![]() 个零点
个零点
综上所述:![]() 在
在![]() 上共有
上共有![]() 个零点
个零点

练习册系列答案
相关题目
【题目】![]() 年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的
年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的![]() 次线上测试成绩进行统计如图所示:
次线上测试成绩进行统计如图所示:
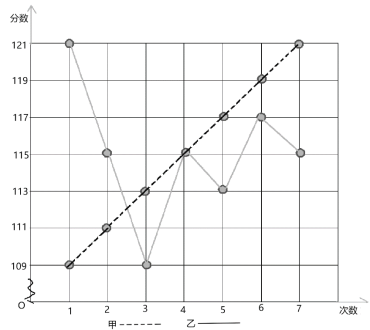
(1)请填写下表(要求写出计算过程)
平均数 | 方差 | |
甲 | ||
乙 |
(2)从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).
【题目】产量相同的机床一和机床二生产同一种零件,在一个小时内生产出的次品数分别记为![]() ,
,![]() ,它们的分布列分别如下:
,它们的分布列分别如下:
| 0 | 1 | 2 | 3 |
| 0.4 | 0.3 | 0.2 | 0.1 |
| 0 | 1 | 2 |
| 0.2 | 0.6 | 0.2 |
(1)哪台机床更好?请说明理由;
(2)记![]() 表示
表示![]() 台机床
台机床![]() 小时内共生产出的次品件数,求
小时内共生产出的次品件数,求![]() 的分布列.
的分布列.