题目内容
已知各项均为正数的数列{ }满足
}满足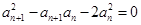 (
(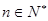 ),且
),且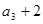 是
是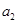 ,
,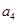 的等差中项.
的等差中项.
(Ⅰ)求数列{ }的通项公式
}的通项公式 ;
;
(Ⅱ)令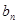 =
=
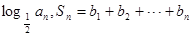 ,是否存在正整数
,是否存在正整数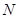 ,使
,使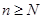 时,不等式
时,不等式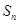
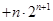
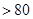 恒成立,若存在,求
恒成立,若存在,求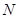 的值;不存在,说明理由.
的值;不存在,说明理由.
 }满足
}满足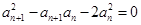 (
(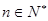 ),且
),且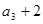 是
是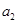 ,
,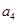 的等差中项.
的等差中项. (Ⅰ)求数列{
 }的通项公式
}的通项公式 ;
;(Ⅱ)令
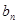 =
=
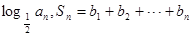 ,是否存在正整数
,是否存在正整数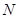 ,使
,使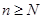 时,不等式
时,不等式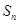
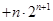
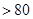 恒成立,若存在,求
恒成立,若存在,求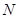 的值;不存在,说明理由.
的值;不存在,说明理由.(Ⅰ) . (Ⅱ)
. (Ⅱ) .
.
 . (Ⅱ)
. (Ⅱ) .
. (1)由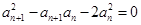 ,得
,得 。
。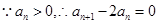 。数列{
。数列{ }是以2为公比的等比数列.根据题意可求得
}是以2为公比的等比数列.根据题意可求得 ,
, (2)由(Ⅰ)及
(2)由(Ⅰ)及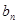 =
=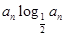 得,
得, 。利用错位相减法求出
。利用错位相减法求出 。要使
。要使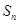
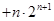
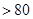 成立,只需
成立,只需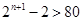 成立,即
成立,即 ,
,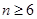 ,取
,取 。
。
(Ⅰ)∵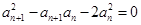 ,
,
∴ ,....................................2分
,....................................2分
∵数列{ }的各项均为正数,∴
}的各项均为正数,∴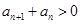 ,
,
∴ ,
,
即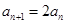 (
(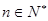 ),所以数列{
),所以数列{ }是以2为公比的等比数列.…………3分
}是以2为公比的等比数列.…………3分
∵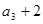 是
是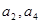 的等差中项,
的等差中项,
∴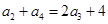 ,∴
,∴ ,∴
,∴ ,
,
∴数列{ }的通项公式
}的通项公式 .……………………………………………………6分
.……………………………………………………6分
(Ⅱ)由(Ⅰ)及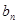 =
=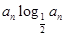 得,
得, , ……………………………8分
, ……………………………8分
∵ ,
,
∴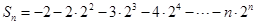 1
1
∴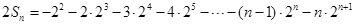 ②
②
②-1得,
=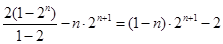 ……………………………10分
……………………………10分
要使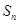
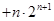
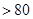 成立,只需
成立,只需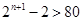 成立,即
成立,即 ,
,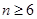 ,
,
使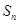
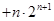
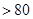 成立,取
成立,取 . …………13分
. …………13分
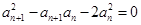 ,得
,得 。
。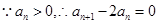 。数列{
。数列{ }是以2为公比的等比数列.根据题意可求得
}是以2为公比的等比数列.根据题意可求得 ,
, (2)由(Ⅰ)及
(2)由(Ⅰ)及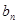 =
=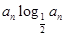 得,
得, 。利用错位相减法求出
。利用错位相减法求出 。要使
。要使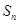
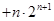
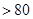 成立,只需
成立,只需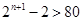 成立,即
成立,即 ,
,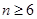 ,取
,取 。
。(Ⅰ)∵
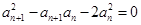 ,
,∴
 ,....................................2分
,....................................2分∵数列{
 }的各项均为正数,∴
}的各项均为正数,∴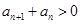 ,
,∴
 ,
,即
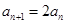 (
(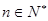 ),所以数列{
),所以数列{ }是以2为公比的等比数列.…………3分
}是以2为公比的等比数列.…………3分∵
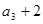 是
是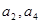 的等差中项,
的等差中项,∴
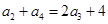 ,∴
,∴ ,∴
,∴ ,
,∴数列{
 }的通项公式
}的通项公式 .……………………………………………………6分
.……………………………………………………6分(Ⅱ)由(Ⅰ)及
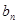 =
=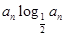 得,
得, , ……………………………8分
, ……………………………8分∵
 ,
,∴
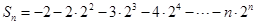 1
1∴
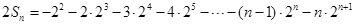 ②
②②-1得,

=
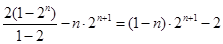 ……………………………10分
……………………………10分要使
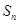
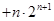
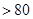 成立,只需
成立,只需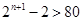 成立,即
成立,即 ,
,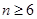 ,
, 使
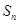
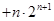
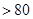 成立,取
成立,取 . …………13分
. …………13分
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
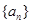 的前
的前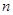 项和
项和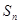 满足
满足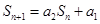 ,其中
,其中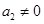
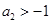 ,求证:
,求证: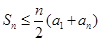 ,并给指出等号成立的充要条件。
,并给指出等号成立的充要条件。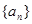 ,满足
,满足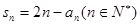
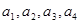 ,并猜想通项公式
,并猜想通项公式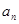 。
。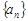 满足:
满足: ;
;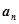 ;(2).令
;(2).令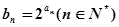 ,求数列
,求数列 的前n项积
的前n项积 。
。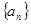 的前
的前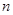 项的和为
项的和为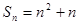 ,
,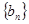 是等比数列,且
是等比数列,且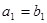 ,
,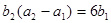 。
。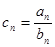 ,求数列
,求数列 的前
的前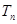 。
。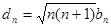 ,数列
,数列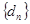 的前
的前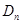 ,求证:
,求证: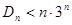 .
.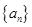 的通项公式
的通项公式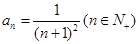 ,
,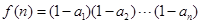 ,试通过计算
,试通过计算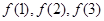 的值,推测出
的值,推测出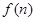 的值。
的值。 中,
中, +
+ +
+ =12,那么
=12,那么 ( )
( )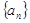 满足
满足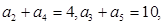 则数列
则数列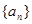 、
、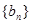 的前n项和分别为
的前n项和分别为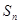 、
、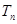 ,若
,若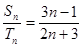 ,则
,则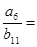 ____________.
____________.