题目内容
数列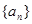 ,满足
,满足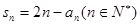
(1)求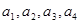 ,并猜想通项公式
,并猜想通项公式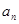 。
。
(2)用数学归纳法证明(1)中的猜想。
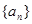 ,满足
,满足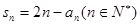
(1)求
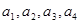 ,并猜想通项公式
,并猜想通项公式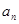 。
。(2)用数学归纳法证明(1)中的猜想。
(1)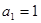 ,
,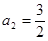 ,
,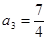 ,
,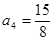 并猜想通项公式
并猜想通项公式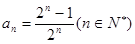 。(2)见解析
。(2)见解析
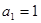 ,
,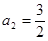 ,
,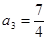 ,
,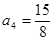 并猜想通项公式
并猜想通项公式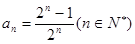 。(2)见解析
。(2)见解析本试题主要考查了数列的通项公式求解,并用数学归纳法加以证明。第一问利用递推关系式得到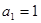 ,
,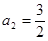 ,
,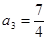 ,
,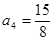 ,并猜想通项公式
,并猜想通项公式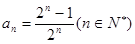
第二问中,用数学归纳法证明(1)中的猜想。
①对n=1,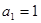 等式成立。
等式成立。
②假设n=k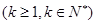 时,
时,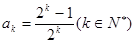 成立,
成立,
那么当n=k+1时,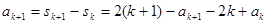
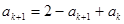 ,所以当n=k+1时结论成立可证。
,所以当n=k+1时结论成立可证。
数列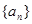 ,满足
,满足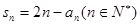
(1)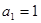 ,
,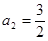 ,
,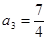 ,
,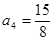 并猜想通项公
并猜想通项公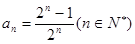 。 …4分
。 …4分
(2)用数学归纳法证明(1)中的猜想。①对n=1,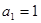 等式成立。 …5分
等式成立。 …5分
②假设n=k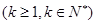 时,
时,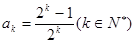 成立,
成立,
那么当n=k+1时,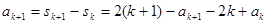
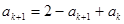 , ……9分
, ……9分
所以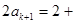
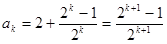
所以当n=k+1时结论成立 ……11分
由①②知,猜想对一切自然数n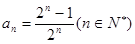 均成立
均成立
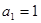 ,
,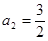 ,
,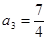 ,
,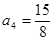 ,并猜想通项公式
,并猜想通项公式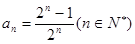
第二问中,用数学归纳法证明(1)中的猜想。
①对n=1,
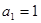 等式成立。
等式成立。②假设n=k
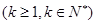 时,
时,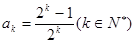 成立,
成立,那么当n=k+1时,
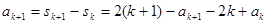
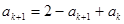 ,所以当n=k+1时结论成立可证。
,所以当n=k+1时结论成立可证。数列
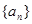 ,满足
,满足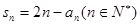
(1)
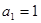 ,
,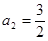 ,
,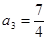 ,
,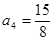 并猜想通项公
并猜想通项公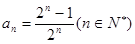 。 …4分
。 …4分(2)用数学归纳法证明(1)中的猜想。①对n=1,
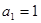 等式成立。 …5分
等式成立。 …5分②假设n=k
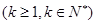 时,
时,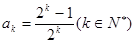 成立,
成立,那么当n=k+1时,
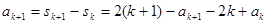
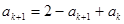 , ……9分
, ……9分所以
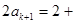
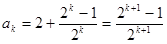
所以当n=k+1时结论成立 ……11分
由①②知,猜想对一切自然数n
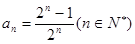 均成立
均成立
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 的前n项和
的前n项和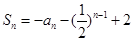 (n为正整数)。
(n为正整数)。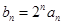 ,求证数列
,求证数列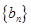 是等差数列,
是等差数列,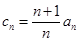 ,
,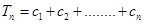 。是否存在最小的正整数
。是否存在最小的正整数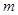 ,使得对于
,使得对于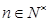 都有
都有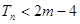 恒成立,若存在,求出
恒成立,若存在,求出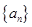 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为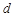 ,
,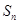 为其前
为其前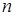 项和,且满足
项和,且满足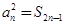 ,
,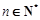 .数列
.数列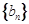 满足
满足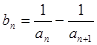 ,
,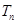 为数列
为数列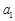 、
、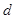 和
和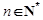 ,不等式
,不等式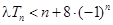 恒成立,求实数
恒成立,求实数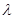 的取值范围
的取值范围 }满足
}满足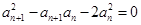 (
(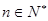 ),且
),且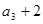 是
是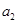 ,
,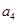 的等差中项.
的等差中项. 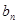 =
=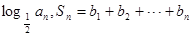 ,是否存在正整数
,是否存在正整数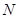 ,使
,使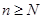 时,不等式
时,不等式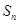
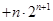
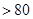 恒成立,若存在,求
恒成立,若存在,求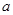 、
、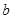 、
、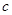 成等差数列,则
成等差数列,则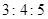 ;
;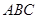 的三内角
的三内角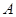 、
、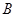 、
、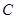 成等差数列,则
成等差数列,则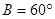 ;
;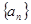 的前
的前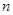 项和为
项和为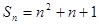 ,则
,则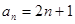 ;
;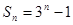 ,则
,则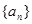 中,
中,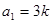 ,其中
,其中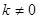 ,对任意
,对任意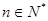 都有:
都有: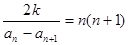 ;(1)求数列
;(1)求数列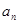 ,假设
,假设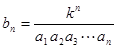 ,试求数列
,试求数列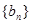 的前
的前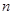 项和
项和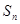 ;
;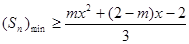 对一切
对一切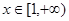 恒成立,求
恒成立,求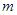 的取值范围。
的取值范围。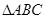 中角
中角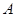 、
、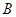 、
、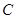 成等差数列,则
成等差数列,则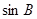 =( )
=( )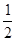
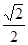
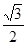
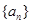 中,
中,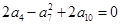 ,则
,则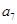 的值为( )
的值为( )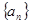 中,如果存在正整数
中,如果存在正整数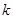 和
和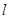 (
(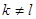 ),使得前
),使得前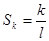 ,前
,前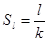 ,则( )
,则( )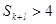
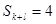
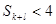
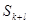 与4的大小关系不确定
与4的大小关系不确定