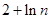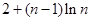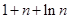题目内容
已知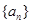 的前
的前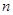 项和
项和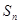 满足
满足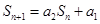 ,其中
,其中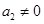
(Ⅰ)求证: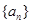 首项为1的等比数列;
首项为1的等比数列;
(Ⅱ)若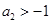 ,求证:
,求证: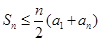 ,并给指出等号成立的充要条件。
,并给指出等号成立的充要条件。
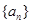 的前
的前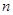 项和
项和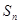 满足
满足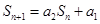 ,其中
,其中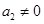
(Ⅰ)求证:
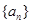 首项为1的等比数列;
首项为1的等比数列;(Ⅱ)若
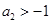 ,求证:
,求证: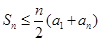 ,并给指出等号成立的充要条件。
,并给指出等号成立的充要条件。见解析
(Ⅰ)由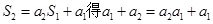 ,即
,即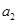
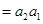 ,
,
因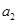
 ,故
,故 ,得
,得
又由题设条件知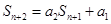 ,
,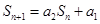
两式相减得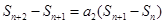 ,即
,即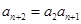 由
由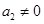 ,知
,知 ,
,
因此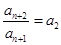 综上
综上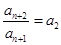 对所有
对所有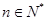 成立,从而
成立,从而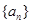 是首项为1,公比为
是首项为1,公比为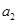 的等比数列。
的等比数列。
(Ⅱ)当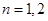 时,显然
时,显然 ,等号成立
,等号成立
设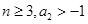 且
且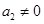 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,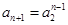 所以要证的不等式化为
所以要证的不等式化为 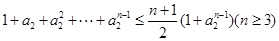
即证: ,当
,当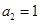 时,上面不等式的等号成立
时,上面不等式的等号成立
当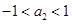 时,
时,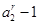 与
与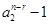
 同为负;当
同为负;当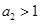 时
时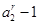
与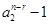
 同为正,因此当
同为正,因此当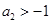 且
且 时,
时,
总有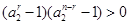 ,即
,即

上面不等式对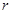 从1到
从1到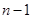 求各得
求各得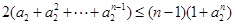
由此得
综上,当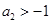 且
且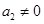 时,有
时,有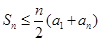 ,当且仅当
,当且仅当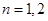 或
或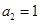 时等号成立。
时等号成立。
【考点定位】本题考查了数列前n项和的概念,不等式恒成立问题,数学归纳法的应用,合理猜想与逻辑推理的概念.对不等式的考查有一定的难度,综合性较强,需要同学有深厚的功底才能胜任本题的解答,对数学归纳法的考查较深
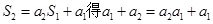 ,即
,即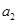
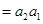 ,
,因
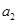
 ,故
,故 ,得
,得
又由题设条件知
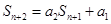 ,
,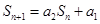
两式相减得
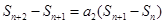 ,即
,即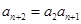 由
由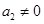 ,知
,知 ,
,因此
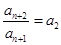 综上
综上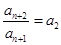 对所有
对所有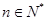 成立,从而
成立,从而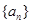 是首项为1,公比为
是首项为1,公比为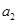 的等比数列。
的等比数列。(Ⅱ)当
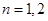 时,显然
时,显然 ,等号成立
,等号成立设
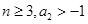 且
且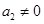 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,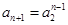 所以要证的不等式化为
所以要证的不等式化为 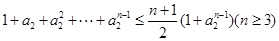
即证:
 ,当
,当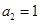 时,上面不等式的等号成立
时,上面不等式的等号成立当
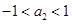 时,
时,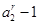 与
与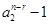
 同为负;当
同为负;当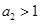 时
时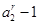
与
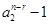
 同为正,因此当
同为正,因此当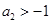 且
且 时,
时,总有
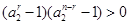 ,即
,即

上面不等式对
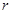 从1到
从1到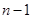 求各得
求各得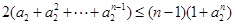
由此得

综上,当
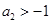 且
且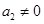 时,有
时,有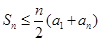 ,当且仅当
,当且仅当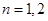 或
或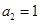 时等号成立。
时等号成立。【考点定位】本题考查了数列前n项和的概念,不等式恒成立问题,数学归纳法的应用,合理猜想与逻辑推理的概念.对不等式的考查有一定的难度,综合性较强,需要同学有深厚的功底才能胜任本题的解答,对数学归纳法的考查较深

练习册系列答案
相关题目
 万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过
万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过 年后该项目的资金为
年后该项目的资金为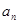 万元.
万元.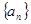 的前三项
的前三项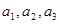 ,并猜想写出通项
,并猜想写出通项 千万元.
千万元.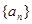 为等差数列,且
为等差数列,且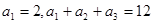 .
.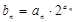 ,求数列
,求数列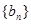 的前
的前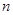 项和
项和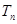 .
. }满足
}满足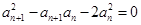 (
(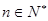 ),且
),且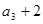 是
是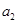 ,
,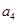 的等差中项.
的等差中项. 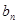 =
=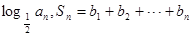 ,是否存在正整数
,是否存在正整数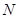 ,使
,使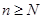 时,不等式
时,不等式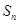
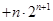
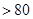 恒成立,若存在,求
恒成立,若存在,求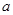 、
、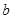 、
、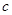 成等差数列,则
成等差数列,则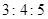 ;
;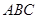 的三内角
的三内角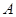 、
、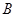 、
、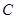 成等差数列,则
成等差数列,则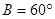 ;
;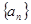 的前
的前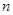 项和为
项和为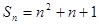 ,则
,则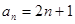 ;
;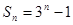 ,则
,则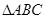 中角
中角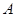 、
、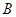 、
、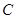 成等差数列,则
成等差数列,则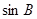 =( )
=( )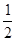
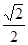
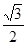
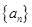 的公差
的公差 ,
,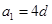 ,若
,若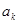 是
是 与
与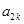 的等比中项,则
的等比中项,则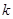 的值为 .
的值为 .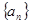 中,如果存在正整数
中,如果存在正整数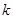 和
和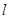 (
(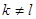 ),使得前
),使得前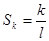 ,前
,前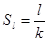 ,则( )
,则( )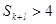
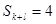
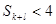
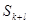 与4的大小关系不确定
与4的大小关系不确定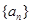 中,
中,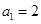 ,
, 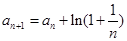 ,则
,则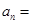 ( )
( )