题目内容
【题目】下列判断正确的是 (把正确的序号都填上).
①若f(x)=ax2+(2a+b)x+2 (其中x∈[2a-1,a+4])是偶函数,则实数b=2;
②若函数![]() 在区间
在区间![]() 上递增,在区间
上递增,在区间![]() 上也递增,则函数
上也递增,则函数![]() 必在
必在![]() 上递增;
上递增;
③f(x)表示-2x+2与-2x2+4x+2中的较小者,则函数f(x)的最大值为1;
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x、y∈R都满足f(x·y)=x·f(y)+y·f(x),则f(x)是奇函数.Ks
【答案】①④
【解析】
试题分析:①由题意得![]() ;②中命题不成立,如
;②中命题不成立,如![]() ;③f(x)表示-2x+2与-2x2+4x+2中的较小者,∴
;③f(x)表示-2x+2与-2x2+4x+2中的较小者,∴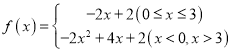 ,∴f(x)的最大值为2,原命题错误;④∵f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),
,∴f(x)的最大值为2,原命题错误;④∵f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),
∴当x=y=1时,f(1)=f(1)+f(1),∴f(1)=0;
当x=y=-1时,f(1)=-f(-1)-f(-1),∴f(-1)=0;
当y=-1时,f(-x)=xf(-1)+[-f(x)],即f(-x)=-f(x),∴f(x)是奇函数,命题正确

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目