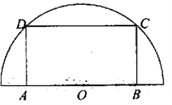
[题目]如图.在半径为的半圆形(为圆心)铝皮上截取一块矩形材料.其中在直径上.点在圆周上.(1)设.将矩形的面积表示成的函数.并写出其定义域,(2)怎样截取.才能使矩形材料的面积最大?并求出最大面积. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在半径为的半圆形（为圆心）铝皮上截取一块矩形材料，其中在直径上，点在圆周上.

（1）设，将矩形的面积表示成的函数，并写出其定义域；

（2）怎样截取，才能使矩形材料的面积最大？并求出最大面积.

【答案】(1)y=2x，x∈（0，20）.(2)截取AD=10时，才能使矩形材料ABCD的面积最大，最大面积为.

【解析】试题分析：（1）根据勾股定理得OA=2，再根据矩形面积公式得函数关系式，最后根据实际意义得定义域；（2）先整理成关于二次函数，再根据二次函数对称轴与定义区间位置关系确定最大值取法

试题解析：（1）AB=2OA=2，∴y=f（x）=2x，x∈（0，20）.

（2）时， .

∴截取AD=10时，才能使矩形材料ABCD的面积最大，最大面积为.

练习册系列答案

相关题目

【题目】设z1 ， z2是复数，则下列命题中的假命题是（）
A.若|z1﹣z2|=0，则 =
B.若z1= ，则 =z2
C.若|z1|=|z2|，则z1 =z2
D.若|z1|=|z2|，则z12=z22

【题目】如图，四边形中，，，，，、分别在、上，，现将四边形沿折起，使平面平面．

（）若，是否存在折叠后的线段上存在一点，且，使得平面？若存在，求出的值；若不存在，说明理由．

（）求三棱锥的体积的最大值，并求此时点到平面的距离．

【题目】解答题
（1）解不等式：|2x﹣1|﹣|x|＜1；
（2）设a2﹣2ab+5b2=4对a，b∈R成立，求a+b的最大值及相应的a，b．

【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点．研究表明：“活水围网”养鱼时，某种鱼在一定的条件下，每尾鱼的平均生长速度（单位：千克/年）是养殖密度（单位：尾/立方米）的函数．当不超过4（尾/立方米）时，的值为（千克/年）；当时，是的一次函数；当达到（尾/立方米）时，因缺氧等原因，的值为（千克/年）．