题目内容
【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN= ![]() BB1 .
BB1 . 
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小.
【答案】
(1)证明:∵四边形BB1C1C是矩形,∴BC⊥BB1,
∵平面BB1C1C⊥底面ABB1N,平面BB1C1C∩底面ABB1N=BB1,BC平面BB1C1C,
∴BC⊥平面ABB1N,
以B为原点,以BA,BB1,BC为坐标轴建立空间直角坐标系B﹣xyz,
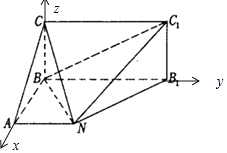
设AB=1,则B(0,0,0),N(1,1,0),B1(0,2,0),C1(0,2,1),C(0,0,1)
∴ ![]() =(1,1,0),
=(1,1,0), ![]() =(﹣1,1,0),
=(﹣1,1,0), ![]() =(0,0,1),
=(0,0,1),
∴ ![]() =﹣1+1=0,
=﹣1+1=0, ![]() =0,
=0,
∴BN⊥NB1,BN⊥B1C1,又NB1∩B1C1=B1,
∴BN⊥平面C1B1N.
(2)解: ![]() =(﹣1,1,1),
=(﹣1,1,1), ![]() =(﹣1,﹣1,1),
=(﹣1,﹣1,1), ![]() =(0,2,0),
=(0,2,0),
设平面BNC1的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 ![]() ,
, ![]() =0,
=0,
∴ ![]() ,令x=1得
,令x=1得 ![]() =(1,﹣1,2),
=(1,﹣1,2),
同理可得平面CNC1的法向量为 ![]() =(1,0,1),
=(1,0,1),
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴二面角C﹣C1N﹣B的大小为30°.
【解析】(1)证明BC⊥平面ABB1N,建立空间坐标系,利用向量证明BN⊥NB1,NB⊥B1C1,故而得出结论;(2)求出两平面的法向量,计算法向量的夹角即可得出二面角的大小.

【题目】医学上所说的“三高”通常是指血脂增高、血压增高、血糖增高等疾病.为了解“三高”疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
(1)请将列联表补充完整;
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(2)能否在犯错误的概率不超过0.005的前提下认为患“三高”疾病与性别有关? 下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() .
.