题目内容
【题目】已知椭圆C的中心在原点O，焦点在x轴上，离心率为 
，左焦点到左顶点的距离为1．
（1）求椭圆C的标准方程；
（2）过点M（1，1）的直线与椭圆C相交于A，B两点，且点M为弦AB中点，求直线AB的方程．
【答案】
（1）解：设椭圆C的方程为 
=1（a＞b＞0），半焦距为c．
依题意e= 
，
由左焦点到左顶点的距离为1，得a﹣c=1．
解得c=1，a=2．∴b2=a2﹣c2=3．
所以椭圆C的标准方程是 
（2）解：设A（x1，y1），B（x2，y2），
∵点M（1，1）为弦AB中点，∴ 
，
把A（x1，y1），B（x2，y2）代入椭圆C的标准方程 ．
得：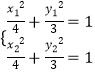 
，∴3（x1+x2）（x1﹣x2）+4（y1+y2）（y1﹣y2）=0，
∴6（x1﹣x2）+8（y1﹣y2）=0，
∴k= 
=﹣ 
，
∴直线AB的方程为y﹣1=﹣ （x﹣1），整理，得：3x+4y﹣7=0．
∴直线AB的方程为：3x+4y﹣7=0
【解析】（1）由椭圆离心率为 
，左焦点到左顶点的距离为1，列出方程组，求出a，b，由此能求出椭圆C的标准方程．（2）设A（x1 ， y1），B（x2 ， y2），由点M（1，1）为弦AB中点，利用点差法能求出直线AB的方程．
【考点精析】通过灵活运用椭圆的标准方程，掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
即可以解答此题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
