题目内容
【题目】定义在R上函数f（x），且f（x）+f（﹣x）=0，当x＜0时，f（x）=（ 
）x﹣8×（ 
）x﹣1
（1）求f（x）的解析式；
（2）当x∈[1，3]时，求f（x）的最大值和最小值．
【答案】
（1）解：f（x）+f（﹣x）=0，则函数f（x）是奇函数，则f（0）=0，（2分）
当x＞0时，﹣x＜0，则 
，
所以 
，
所以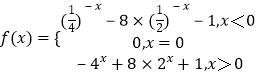 
（2）解：令t=2x，则t∈[2，8]，y=﹣t2+8t+1t∈[2，8]，
对称轴为t=4∈[2，8]，
当t=4，即x=2，f（x）max=﹣16+32+1=17；
当t=8，即x=3，f（x）min=﹣64+64+1=1．
【解析】（1）确定f（0）=0，当x＞0时，﹣x＜0，利用当x＜0时，f（x）=（ 
）x﹣8×（ 
）x﹣1，求出函数的解析式，即可求f（x）的解析式；（2）当x∈[1，3]时，换元，利用配方法求f（x）的最大值和最小值．
练习册系列答案
特高级教师点拨系列答案
相关题目
