题目内容
17.设有甲乙两个公司,甲公司的资产数为800万,资产年增长率为18%,乙公司的资产数为1200万,资产的年增长率为8%,设若干年内两公司的资产增长率不变.(1)试建立这两个公司资产y与经过年数的函数关系;
(2)试预测经过多少年后,甲公司的资产数超过乙公司的资产数(x∈N*)
分析 (1)根据甲乙的年增长率,建立条件关系即可.
(2)假设经过x年后,甲公司的资产数超过乙公司的资产数(x∈N*),解不等式即可.
解答 解:(1)∵甲公司的资产数为800万,资产年增长率为18%,
∴y=800(1+18%)x=800×1.18x,
∵乙公司的资产数为1200万,资产的年增长率为8%,
∴y=1200(1+8%)x=1200×1.08x.
(2)假设经过x年后,甲公司的资产数超过乙公司的资产数(x∈N*),
即800×1.18x>1200×1.08x,
即1.18x>$\frac{3}{2}$×1.08x,
等式两边取对数得xlg1.18>lg$\frac{3}{2}$+xlg1.18,
即x(lg1.18-lg1.08)>lg$\frac{3}{2}$,
即xlg$\frac{118}{108}$>lg$\frac{3}{2}$,
即x>$\frac{lg\frac{3}{2}}{lg\frac{118}{108}}$=$\frac{lg3-lg2}{lg118-lg108}$≈4.58,
∵x∈N*,
∴x=5,
即经过5年后,甲公司的资产数超过乙公司的资产数.
点评 本题主要考查函数的应用问题,根据条件建立函数关系是解决本题的关键.

练习册系列答案
相关题目
8.已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则( )
| A. | ab≤$\frac{1}{8}$ | B. | ab≥$\frac{1}{8}$ | C. | ab$≥\frac{1}{4}$ | D. | ab$≤\frac{1}{4}$ |
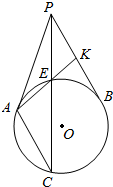 如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.
如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.