题目内容
7．已知一元二次方程x2+（a2-9）x+a2-5a+6=0一个根小于0，另一根大于2，求a的取值范围．分析 设f（x）=x2+（a2-9）x+a2-5a+6，则由题意可得$\left\{\begin{array}{l}{f（0）{=a}^{2}-5a+6＜0}\\{f（2）={3a}^{2}-5a-8＜0}\end{array}\right.$，由此求得a的范围．
解答 解：设f（x）=x2+（a2-9）x+a2-5a+6，则由题意可得$\left\{\begin{array}{l}{f（0）{=a}^{2}-5a+6＜0}\\{f（2）={3a}^{2}-5a-8＜0}\end{array}\right.$，
求得 2＜a＜$\frac{8}{3}$．
点评 本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
15．设A（-2，3），B（3，3），若直线ax+y+2=0与线段AB有交点，则实数a的取值范围是（ ）
| A． | [-$\frac{5}{3}$，$\frac{5}{2}$] | B． | （-∞，-$\frac{5}{3}$]∪[$\frac{5}{2}$，+∞） | C． | （-∞，-$\frac{5}{2}$]∪[$\frac{5}{3}$，+∞） | D． | [-$\frac{5}{2}$，$\frac{5}{3}$] |
12．函数y=log${\;}_{\frac{1}{2}}$（1-2x）的值域为（ ）
| A． | （-∞，+∞） | B． | （-∞，0） | C． | （0，+∞） | D． | （1，+∞） |
16．图是截去了一个角的正方体，则它的俯视图为（ ）
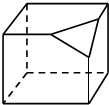
| A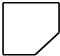． |  | B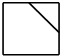． |  | C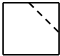． |  | D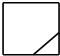． |  |