题目内容
6.等差数列{an}中,a1=-3,11a5=5a8-13.(1)求公差d;
(2)求前n项和Sn最小值.
分析 (1)由已知条件利用等差数列的通项公式求出首项与公差;
(2)求出Sn,再利用配方法能求出Sn的最小值.
解答 解:(1)∵在等差数列{an}中,a1=-3,11a5=5a8-13,
∴由题意知11(-3+4d)=5(-3+7d)-13,
解得d=$\frac{5}{9}$,
(2)Sn=-3n+$\frac{n(n-1)}{2}$×$\frac{5}{9}$
=$\frac{5{n}^{2}}{18}$-$\frac{59}{18}$n
=$\frac{5}{18}$(n-$\frac{59}{10}$)2-$\frac{3481}{360}$,
∴n=6时,Sn取最小值S6=-$\frac{29}{3}$.
点评 本题考查数列{an}的前n项和Sn的最小值的求法,解题时要注意等差数列的性质和配方法的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.参数方程$\left\{\begin{array}{l}{x=2+si{n}^{2}θ}\\{y=-1+2co{s}^{2}θ}\end{array}\right.$(θ为参数)化为普通方程是( )
| A. | 2x-y+5=0 | B. | 2x+y-5=0 | C. | 2x-y+5=0(2≤x≤3) | D. | 2x+y-5=0(2≤x≤3) |
14.已知方程x2-5x-8=0的两个根为x1,x2,求作一个新的一元二次方程,使它的两根分别为$\frac{{x}_{1}}{{x}_{2}}$和$\frac{{x}_{2}}{{x}_{1}}$.
18.方程-sinx=($\frac{1}{2}$)x在区间(0,100π)内解的个数是( )
| A. | 98 | B. | 100 | C. | 102 | D. | 200 |
15.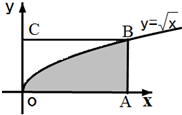 如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )
如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )
 如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )
如图,长方形的四个顶点为O(0,0),A(4,0),B(4,2),C(0,2),曲线$y=\sqrt{x}$经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{7}{12}$ |