Question

【题目】函数f（x）= e3x+me2x+（2m+1）ex+1有两个极值点，则实数m的取值范围是（ ）
A.（﹣ ，1﹣ ）
B.[﹣ ，1﹣ ]
C.（﹣∞，1﹣ ）
D.（﹣∞，1﹣ ）∪（1+ ，+∞）

Answer 1

【答案】A
【解析】解：令t=ex，则t＞0，

则y=f（x）= e3x+me2x+（2m+1）ex+1，可化为：

y=g（t）= ，

则g′（t）=t2+2mt+2m+1，

若函数f（x）= e3x+me2x+（2m+1）ex+1有两个极值点，

则g′（t）=t2+2mt+2m+1=0有两个正根，

∴ ，

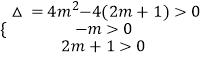解得：m∈（﹣ ，1﹣ ），

故选：A

【考点精析】认真审题，首先需要了解函数的极值与导数(求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值)．