题目内容
【题目】已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
x | 3 | ﹣2 | 4 |
|
y | ﹣2 | 0 | ﹣4 |
|
(1)求C1、C2的标准方程;
(2)请问是否存在直线l满足条件:①过C2的焦点F;②与C1交不同两点M、N且满足 ![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
【答案】
(1)解:设抛物线C2:y2=2px(p≠0),则有 ![]() ,据此验证4个点知(3,﹣2
,据此验证4个点知(3,﹣2 ![]() )、(4,﹣4)在抛物线上,易求C2:y2=4x
)、(4,﹣4)在抛物线上,易求C2:y2=4x
设C1: ![]() ,把点(﹣2,0)(
,把点(﹣2,0)( ![]() )代入得:
)代入得:
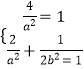 解得
解得 ![]()
∴C1方程为 ![]()
(2)解:容易验证直线l的斜率不存在时,不满足题意;
当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),
设其方程为y=k(x﹣1),与C1的交点坐标为M(x1,y1),N(x2,y2)
由 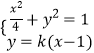 消掉y,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,
消掉y,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,
于是 ![]() ,
, ![]() ①
①
y1y2=k(x1﹣1)×k(x1﹣1)=k2[x1x2﹣(x1+x2)+1]
即 ![]() ②
②
由 ![]() ,即
,即 ![]() ,得x1x2+y1y2=0(*),
,得x1x2+y1y2=0(*),
将①、②代入(*)式,得 ![]() ,解得k=±2;
,解得k=±2;
所以存在直线l满足条件,且l的方程为:y=2x﹣2或y=﹣2x+2.
【解析】(1)设抛物线C2:y2=2px(p≠0),则有 ![]() ,据此验证4个点知(3,﹣2
,据此验证4个点知(3,﹣2 ![]() )、(4,﹣4)在抛物线上,易求C2:y2=4x,设C1:
)、(4,﹣4)在抛物线上,易求C2:y2=4x,设C1: ![]() ,把点(﹣2,0)(
,把点(﹣2,0)( ![]() )代入得:
)代入得: 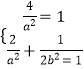 ,由此能够求出C1方程.(2)容易验证直线l的斜率不存在时,不满足题意;当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),
,由此能够求出C1方程.(2)容易验证直线l的斜率不存在时,不满足题意;当直线l斜率存在时,假设存在直线l过抛物线焦点F(1,0),
设其方程为y=k(x﹣1),与C1的交点坐标为M(x1 , y1),N(x2 , y2),由 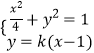 消掉y,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,再由韦达定理能够导出存在直线l满足条件,且l的方程为:y=2x﹣2或y=﹣2x+2.
消掉y,得(1+4k2)x2﹣8k2x+4(k2﹣1)=0,再由韦达定理能够导出存在直线l满足条件,且l的方程为:y=2x﹣2或y=﹣2x+2.
【考点精析】根据题目的已知条件,利用椭圆的标准方程的相关知识可以得到问题的答案,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
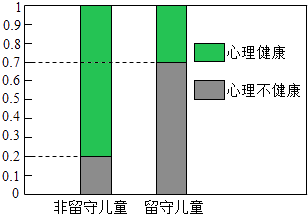
小学生10分钟应用题系列答案【题目】为研究心理健康与是否是留守儿童的关系,某小学在本校四年级学生中抽取了一个110人的样本,其中留守儿童有40人,非留守儿童有70人,对他们进行了心理测试,并绘制了如图的等高条形图,试问:能否在犯错误的概率不超过0.001的前提下认为心理健康与是否是留守儿童有关系?
参考数据:
P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() (n=a+b+c+d)
(n=a+b+c+d)