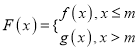题目内容
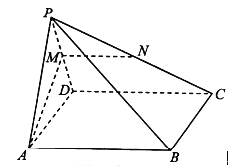
【题目】已知直角△ABC，AB=AC=3，P，Q分别为边AB，BC上的点，M，N是平面上两点，若 
+ 
=0，（ 
+ 
） 
=0， 
=3 
，且直线MN经过△ABC的外心，则 
=（ ）
A.
B.
C.1
D.2
【答案】D
【解析】解：建立坐标系将，将直角三角形放入坐标系中，
若 
+ 
=0，则 =﹣ = 
，
即A是PM的中点，
∵直线MN经过△ABC的外心，
∴直线MN经过BC的中点E，
∵（ 
+ 
） 
=0，
∴ 
=0，即PQ⊥BC，AE⊥BC，
则PN∥AE，PN=2AE=2×3 
=6 ，
∵ 
=3 ，
∴PN=3PQ=6 ，
即PQ=2 ，
直线BC的方程为x+y﹣3=0，
设P（0，m），0＜m＜3，
则PQ= 
，即|m﹣3|=2，
则m=1或m=5（舍），
即P（0，1），则 
=|BP|=2，
故选：D．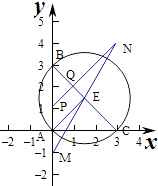
练习册系列答案
相关题目
【题目】已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点O，从每条曲线上取两个点，将其坐标记录于下表中：
x | 3 | ﹣2 | 4 |
|
y | ﹣2 | 0 | ﹣4 |
|
（1）求C1、C2的标准方程；
（2）请问是否存在直线l满足条件：①过C2的焦点F；②与C1交不同两点M、N且满足 
？若存在，求出直线l的方程；若不存在，说明理由．
