题目内容
已知直线l1过点B(0,-6)且与直线2x-3λy=0平行,直线l2经过定点A(0,6)且斜率为-
,直线l1与l2相交于点P,其中λ∈R,
(1)当λ=1时,求点P的坐标.
(2)试问:是否存在两个定点E、F,使得|PE|+|PF|为定值,若存在,求出E、F的坐标,若不存在,说明理由.
| 2λ |
| 3 |
(1)当λ=1时,求点P的坐标.
(2)试问:是否存在两个定点E、F,使得|PE|+|PF|为定值,若存在,求出E、F的坐标,若不存在,说明理由.
(1)当λ=1时,直线2x-3λy=0即2x--3y=0,
∵l1与此直线平行,∴可设直线l1的方程为2x-3y+c=0,
又直线l1过点B(0,-6),将其代入得0-3×(-6)+c=0,解得c=-18.∴直线l1的方程为 2x-3y-18=0.
∵直线l2经过定点A(0,6)且斜率为-
,即-
,∴直线l2的方程为y-6=-
x,即2x+3y-18=0.
联立
解得
.即点P(9,0).
(2)∵直线l1与直线2x-3λy=0平行,∴当λ≠0时,直线l1的斜率为
,
而直线l2斜率为-
,又
×(-
)=-
.
设点P(x,y),则KPB×KPA=-
,于是
×
=-
(x≠0),化为
+
=1(x≠0).
当λ=0时,直线l1即为y轴,直线l2即为y=6,
∴二直线交于点(0,6),
∴点P的轨迹为椭圆
+
=1(去掉点(0,-6)).
综上可知:取点E(3
,0),F(-3
,0),则满足|PE|+|PF|为定值.
∵l1与此直线平行,∴可设直线l1的方程为2x-3y+c=0,
又直线l1过点B(0,-6),将其代入得0-3×(-6)+c=0,解得c=-18.∴直线l1的方程为 2x-3y-18=0.
∵直线l2经过定点A(0,6)且斜率为-
| 2λ |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
联立
|
|
(2)∵直线l1与直线2x-3λy=0平行,∴当λ≠0时,直线l1的斜率为
| 2 |
| 3λ |
而直线l2斜率为-
| 2λ |
| 3 |
| 2 |
| 3λ |
| 2λ |
| 3 |
| 4 |
| 9 |
设点P(x,y),则KPB×KPA=-
| 4 |
| 9 |
| y+6 |
| x |
| y-6 |
| x |
| 4 |
| 9 |
| x2 |
| 81 |
| y2 |
| 36 |
当λ=0时,直线l1即为y轴,直线l2即为y=6,
∴二直线交于点(0,6),
∴点P的轨迹为椭圆
| x2 |
| 81 |
| y2 |
| 36 |
综上可知:取点E(3
| 5 |
| 5 |

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
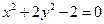 的两焦点为
的两焦点为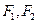 ,
,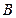 为短轴的一个端点,则
为短轴的一个端点,则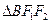 的外接圆的方程是 。
的外接圆的方程是 。 的右焦点为
的右焦点为 ,右准线与
,右准线与 轴交于点
轴交于点 ,若椭圆的离心率
,若椭圆的离心率
 的值
的值 两点,且
两点,且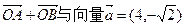 共线(
共线( 为坐标原点)求
为坐标原点)求 的夹角
的夹角 的焦点为
的焦点为 ,点P为其上的动点,当
,点P为其上的动点,当 为钝角时,点P横坐标的取值范围是_________;
为钝角时,点P横坐标的取值范围是_________; 为常数,且
为常数,且 ,过点
,过点 且以向量
且以向量 为方向向量的直线与椭圆交于点
为方向向量的直线与椭圆交于点 ,直线
,直线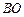 交椭圆于点
交椭圆于点 (
( 为坐标原点).(1)
为坐标原点).(1) 的面积
的面积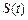 的表达式;(2)若
的表达式;(2)若 ,求
,求