题目内容
(12分)定义在区间(-1,1)上的函数f (x)满足:①对任意的x,y∈(-1,1),都有f (x) + f (y) =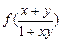 ; ②当x∈(-1,0),f (x) > 0.
; ②当x∈(-1,0),f (x) > 0.
(1)求证f (x)为奇函数;
(2)试解不等式:f (x) + f (x-1)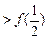 .
.
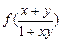 ; ②当x∈(-1,0),f (x) > 0.
; ②当x∈(-1,0),f (x) > 0. (1)求证f (x)为奇函数;
(2)试解不等式:f (x) + f (x-1)
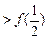 .
.(1)略
(2)不等式的解集为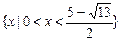
(2)不等式的解集为
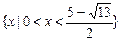
解:(1)解:令x = y = 0,则
f (0) + f (0) =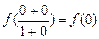 ∴ f (0) = 0
∴ f (0) = 0
令x∈(-1, 1) ∴-x∈(-1, 1)
∴ f (x) + f (-x) = f (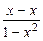 ) = f (0) = 0
) = f (0) = 0
∴ f (-x) =-f (x)
∴ f (x) 在(-1,1)上为奇函数…………………4分
(2)解:令-1< x1 < x2 < 1
则f (x1) -f (x2) = f (x1) + f (-x2) =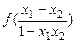
∵x1-x2 < 0,1-x1x2 > 0
∴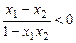 ∴
∴ 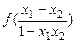 > 0
> 0
∴ f (x1) > f (x2) ∴ f (x) 在(-1,1)上为减函数
又f (x) + f (x-1) >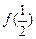

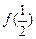 …………………8分
…………………8分
∴ 不等式化 为
为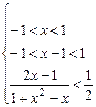
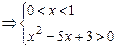
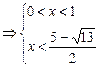 或
或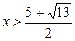
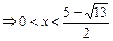
∴ 不等式的解集为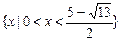 …………………12分
…………………12分
f (0) + f (0) =
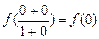 ∴ f (0) = 0
∴ f (0) = 0令x∈(-1, 1) ∴-x∈(-1, 1)
∴ f (x) + f (-x) = f (
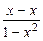 ) = f (0) = 0
) = f (0) = 0∴ f (-x) =-f (x)
∴ f (x) 在(-1,1)上为奇函数…………………4分
(2)解:令-1< x1 < x2 < 1
则f (x1) -f (x2) = f (x1) + f (-x2) =
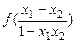
∵x1-x2 < 0,1-x1x2 > 0
∴
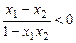 ∴
∴ 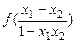 > 0
> 0∴ f (x1) > f (x2) ∴ f (x) 在(-1,1)上为减函数
又f (x) + f (x-1) >
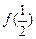

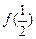 …………………8分
…………………8分∴ 不等式化
 为
为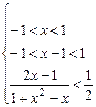
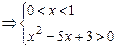
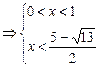 或
或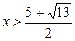
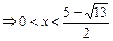
∴ 不等式的解集为
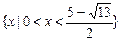 …………………12分
…………………12分
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
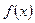 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(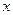 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式:
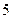 分钟与开讲
分钟与开讲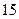 分钟比较,学生的接受能力何时强一些?
分钟比较,学生的接受能力何时强一些?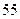 的接受能力以及
的接受能力以及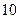 分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?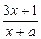 (x≠-a,a≠
(x≠-a,a≠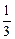 ).
).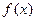 的图象关于y=x对称,求a的值.。
的图象关于y=x对称,求a的值.。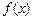 的定义域为R, 对任意实数
的定义域为R, 对任意实数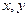 都有
都有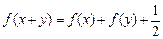 ,
, 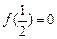 , 当
, 当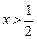 时,
时,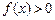 .
.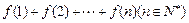 ;
;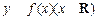 满足
满足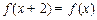 ,且当
,且当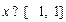 时,
时,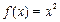 ,则
,则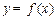 与
与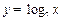 的图象的交点个数为( )
的图象的交点个数为( )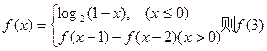 = .
= . ,
, ,且
,且 满足
满足 ,若
,若 的最大值和最小值分别为M、N,则M+N=( )
的最大值和最小值分别为M、N,则M+N=( )
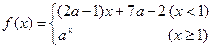 ,在(-∞,+∞)上单调递减,则实数a的取值范围是
,在(-∞,+∞)上单调递减,则实数a的取值范围是  是奇函数,它们的定域
是奇函数,它们的定域 ,且它们在
,且它们在 上的图象如图所示,则不等式
上的图象如图所示,则不等式 的解集是 .
的解集是 .