题目内容
(本小题满分14分)
椭圆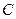 :
: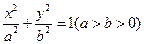 的离心率为
的离心率为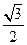 ,长
,长 轴端点与短轴端点间的距离为
轴端点与短轴端点间的距离为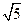 。
。
(I)求椭圆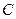 的方程;
的方程;
(II)设过点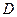
 的直线
的直线 与椭圆
与椭圆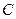 交于
交于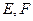 两点,
两点,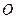 为坐标原点,若
为坐标原点,若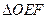
为直角三角形,求直线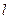 的斜率。
的斜率。
椭圆
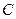 :
: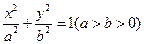 的离心率为
的离心率为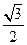 ,长
,长 轴端点与短轴端点间的距离为
轴端点与短轴端点间的距离为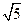 。
。(I)求椭圆
 的方程;
的方程;(II)设过点
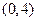
 的直线
的直线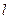 与椭圆
与椭圆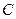 交于
交于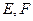 两点,
两点,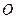 为坐标原点,若
为坐标原点,若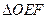
为直角三角形,求直线
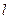 的斜率。
的斜率。(I)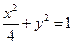
(II)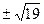 和
和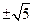
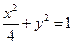
(II)
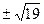 和
和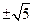
(I)由已知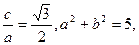 ………………3分
………………3分
又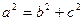 ,解得
,解得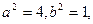
所以椭圆C的方程为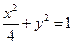 。 ………………………………5分
。 ………………………………5分
(II)根据题意,过点D(0,4)满足题意的直线斜率存在,设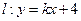 。
。
联立,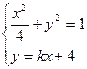 ,消去y得
,消去y得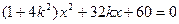 ,…………6分
,…………6分
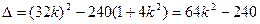 ,
,
令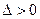 ,解得
,解得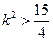 。 ………………………………………………7分
。 ………………………………………………7分
设E、F两点的坐标分别为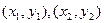 ,
,
(i)当∠EOF为直角时,
则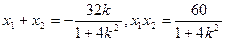 ,…………………………8分
,…………………………8分
因为∠EOF为直角,所以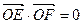 ,即
,即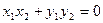 ,………………9分
,………………9分
所以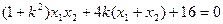 ,
,
所以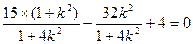 ,解得
,解得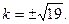 ………………11分
………………11分
(ii)当∠OEF或∠OFE为直角时,不妨设∠OEF为直角,
此时,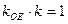 ,所以
,所以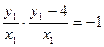 ,即
,即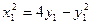 ……①…………12分
……①…………12分
又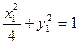 …………②
…………②
将①代入②,消去x1得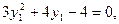
解得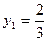 或
或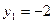 (舍去),……………………13分
(舍去),……………………13分
将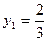 代入①,得
代入①,得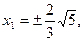 所以
所以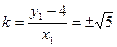 ,………………14分
,………………14分
经检验,所求k值均符合题意,综上,k的值为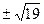 和
和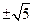 。
。
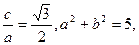 ………………3分
………………3分又
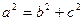 ,解得
,解得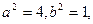
所以椭圆C的方程为
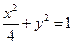 。 ………………………………5分
。 ………………………………5分(II)根据题意,过点D(0,4)满足题意的直线斜率存在,设
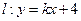 。
。联立,
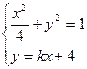 ,消去y得
,消去y得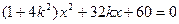 ,…………6分
,…………6分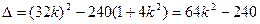 ,
,令
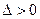 ,解得
,解得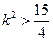 。 ………………………………………………7分
。 ………………………………………………7分设E、F两点的坐标分别为
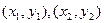 ,
,(i)当∠EOF为直角时,
则
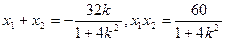 ,…………………………8分
,…………………………8分因为∠EOF为直角,所以
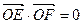 ,即
,即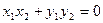 ,………………9分
,………………9分所以
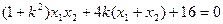 ,
,所以
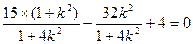 ,解得
,解得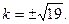 ………………11分
………………11分(ii)当∠OEF或∠OFE为直角时,不妨设∠OEF为直角,
此时,
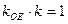 ,所以
,所以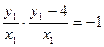 ,即
,即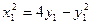 ……①…………12分
……①…………12分又
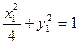 …………②
…………②将①代入②,消去x1得
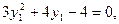
解得
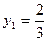 或
或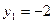 (舍去),……………………13分
(舍去),……………………13分将
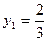 代入①,得
代入①,得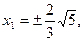 所以
所以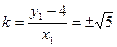 ,………………14分
,………………14分经检验,所求k值均符合题意,综上,k的值为
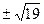 和
和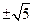 。
。
练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 :
: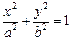 (
(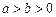 ),其左、右焦点分别为
),其左、右焦点分别为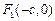 、
、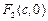 ,且
,且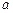 、
、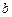 、
、 成等比数列.
成等比数列.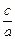 的值.
的值.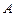 、
、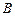 ,求证:
,求证: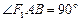 .
.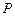 为椭圆
为椭圆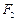 、
、 ,使
,使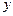 轴的交点
轴的交点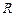 满足
满足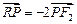 ?若存在,求直线
?若存在,求直线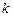 ;若不存在,请说明理由.
;若不存在,请说明理由. B.
B.
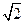 D.
D.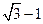

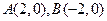 ,
,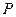 是平面内一动点,直线
是平面内一动点,直线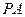 、
、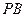 斜率之积为
斜率之积为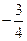 。
。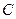 的方程;
的方程;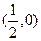 作直线
作直线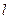 与轨迹
与轨迹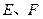 两点,线段
两点,线段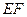 的中点为
的中点为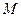 ,求直线
,求直线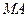 的斜率
的斜率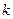 的取值范围。
的取值范围。

 B
B 
 D
D 
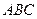 的重心
的重心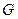 任作一直线分别交
任作一直线分别交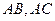 于
于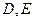 ,
,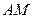 为中线
为中线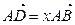 ,
,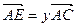 ,
,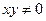 ,求
,求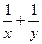 的值
的值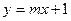 与双曲线
与双曲线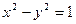 有两个不同的公共点,则实数
有两个不同的公共点,则实数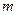 的取值范围是
的取值范围是 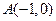 、
、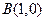 两定点,且以圆
两定点,且以圆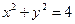 的任一条切线
的任一条切线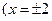 除外)为准线,则该抛物线的焦点F的轨迹方程为: ;
除外)为准线,则该抛物线的焦点F的轨迹方程为: ;