题目内容
【题目】已知函数f(x)=log4(4x+1)+kx,(k∈R)为偶函数.
(1)求k的值;
(2)若方程f(x)=log4(a2x﹣a)有且只有一个根,求实数a的取值范围.
【答案】解:(I) 由题意得f(﹣x)=f(x),
即![]() ,
,
化简得![]() =2kx,
=2kx,
从而4(2k+1)x=1,此式在x∈R上恒成立,
∴k=-![]()
(II)由题意,原方程化为![]() 且a2x﹣a>0
且a2x﹣a>0
即:令2x=t>0![]()
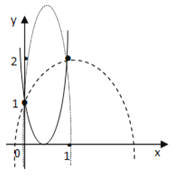
函数y=(1﹣a)t2+at+1的图象过定点(0,1),(1,2)如图所示:
若方程(1)仅有一正根,只有如图的三种情况,
可见:a>1,即二次函数y=(1﹣a)t2+at+1的
开口向下都可,且该正根都大于1,满足不等式(2),
当二次函数y=(1﹣a)t2+at+1的开口向上,
只能是与x轴相切的时候,
此时a<1且△=0,即a=-2-2![]() 也满足不等式(2)
也满足不等式(2)
综上:a>1或a=-2-2![]()
【解析】(Ⅰ)根据偶函数可知f(x)=f(﹣x),取x=﹣1代入即可求出k的值;
(Ⅱ)根据方程![]() 有且只有一个实根,化简可得
有且只有一个实根,化简可得![]() 有且只有一个实根,令t=2x>0,则转化成新方程有且只有一个正根,结合函数的图象讨论a的取值,即可求出实数a的取值范围.
有且只有一个实根,令t=2x>0,则转化成新方程有且只有一个正根,结合函数的图象讨论a的取值,即可求出实数a的取值范围.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段,下表是初赛成绩(得分均为整数,满分为100分)的频率分布表.
分组(分数段) | 频数(人数) | 频率 |
|
| 0.16 |
| 17 |
|
| 19 | 0.38 |
|
|
|
合计 | 50 | 1 |
(Ⅰ)求频率分布表中![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)决赛规则如下:参加决赛的每位同学依次口答3道判断题,答对3道题获得一等奖,答对2道题获得二等奖,答对1道题获得三等奖,否则不得奖.若某同学进入决赛,且其每次答题回答正确与否均是等可能的,试列出他回答问题的所有可能情况,并求出他至少获得二等奖的概率.