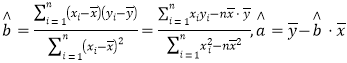题目内容
【题目】在直角坐标系
中，直线
的参数方程为
为参数）,以坐标原点
为极点，
轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线C的极坐标方程为
．
（1）求直线和曲线C的直角坐标方程；
（2）若点P为曲线C上任一点，求点P到直线的距离的最大值，并求此时点P的坐标．
【答案】（1）
,
；（2）
，
．
【解析】
（1）将直线
消参即可得到直线的直角坐标方程，利用公式
化简即可得出答案。
（2）写出曲线
的参数方程，再代入点到直线的距离公式
，化简计算即可得出最大值，以及此时的P点的坐标。
（1）将直线的参数方程消去参数
可得直线的直角坐标方程为．
将
代入曲线C的极坐标得
，即，
故曲线的直角坐标方程为．
（2）设曲线C的参数方程为
（
为参数，
），
则点P的坐标为
，
所以点P到直线的距离为
，
当
时，点P到直线的距离取得最大值，最大值为，
此时
，点P的坐标为．
练习册系列答案
相关题目
【题目】禽流感一直在威胁我们的生活，某疾病控制中心为了研究禽流感病毒繁殖个数
（个）随时间
（天）变化的规律，收集数据如下：
天数 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散点图可看出样本点分布在一条指数型函数
的周围.
保留小数点后两位数的参考数据：
，
，
，
，
，
，
，
，其中
（1）求出关于的回归方程（保留小数点后两位数字）；
（2）已知
，估算第四天的残差.
参考公式：
