题目内容
正三角形的一个顶点位于原点,另外两个顶点在抛物线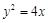 上,则这个正三角形的边长为( )
上,则这个正三角形的边长为( )
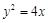 上,则这个正三角形的边长为( )
上,则这个正三角形的边长为( )A.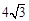 | B.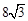 | C.8 | D.16 |
B
分析:设另外两个顶点的坐标分别为 ( , m),(
, m),( , -m),由图形的对称性可以得到方程tan30°=
, -m),由图形的对称性可以得到方程tan30°=  ,解此方程得到m的值.
,解此方程得到m的值.
解答:解:由题意,依据抛物线的对称性,及正三角形的一个顶点位于原点,另外两个顶点在抛物线y2=4x上,可设另外两个顶点的坐标分别为 ( , m),(
, m),( , -m),
, -m),
∴tan30°=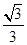 =
= ,
,
解得m=4 ,故这个正三角形的边长为2m=8
,故这个正三角形的边长为2m=8 ,
,
故答案为:B
 , m),(
, m),( , -m),由图形的对称性可以得到方程tan30°=
, -m),由图形的对称性可以得到方程tan30°=  ,解此方程得到m的值.
,解此方程得到m的值.解答:解:由题意,依据抛物线的对称性,及正三角形的一个顶点位于原点,另外两个顶点在抛物线y2=4x上,可设另外两个顶点的坐标分别为 (
 , m),(
, m),( , -m),
, -m),∴tan30°=
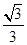 =
= ,
,解得m=4
 ,故这个正三角形的边长为2m=8
,故这个正三角形的边长为2m=8 ,
,故答案为:B

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
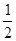 B.x=
B.x=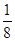 D.y=-
D.y=-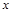 .
.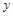 满足方程
满足方程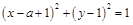 ,当
,当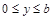 (
(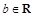 )时,由此方程可以确定一个偶函数
)时,由此方程可以确定一个偶函数 ,则抛物线
,则抛物线 的焦点
的焦点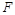 到点
到点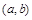 的轨迹上点的距离最大值为_________.
的轨迹上点的距离最大值为_________.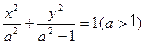 的左右焦点为
的左右焦点为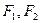 ,抛物线C:
,抛物线C: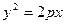 以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。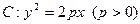 过点
过点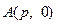 的直线与抛物线C交于M,N两点,且
的直线与抛物线C交于M,N两点,且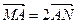 ,过点M,N向直线
,过点M,N向直线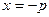 作垂线,垂足分别为
作垂线,垂足分别为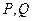 ,
,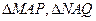 的面积分别为记为
的面积分别为记为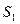 与
与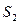 ,
,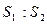 =2:1
=2:1 分抛物线
分抛物线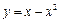 与x轴所围图形为面积相等的两部分,求k的值.
与x轴所围图形为面积相等的两部分,求k的值.
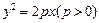 的焦点
的焦点 为双曲线
为双曲线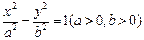 的一个焦点,经过两曲线交点的直线恰好过点
的一个焦点,经过两曲线交点的直线恰好过点

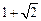
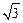
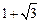
 ,点
,点 是其准线与
是其准线与 轴的焦点,过
轴的焦点,过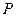 的直线
的直线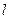 与抛物线
与抛物线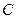 交于
交于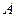 、
、 两点
两点 ,
,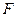 为抛物线
为抛物线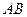 的中点在直线
的中点在直线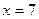 上时,求直线
上时,求直线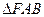 的面积.
的面积. 焦点的直线依次交抛物线与圆
焦点的直线依次交抛物线与圆 于点A、B、C、D,则
于点A、B、C、D,则 的值是( )
的值是( )