题目内容
已知函数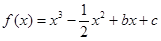 。
。
(Ⅰ)若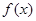 在
在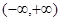 是增函数,求b的取值范围;
是增函数,求b的取值范围;
(Ⅱ)若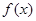 在
在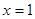 时取得极值,且
时取得极值,且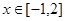 时,
时, 恒成立,求c的取值范围.
恒成立,求c的取值范围.
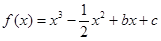 。
。(Ⅰ)若
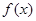 在
在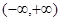 是增函数,求b的取值范围;
是增函数,求b的取值范围;(Ⅱ)若
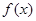 在
在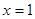 时取得极值,且
时取得极值,且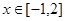 时,
时, 恒成立,求c的取值范围.
恒成立,求c的取值范围.(Ⅰ)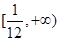 ;(Ⅱ)
;(Ⅱ)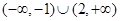 .
.
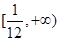 ;(Ⅱ)
;(Ⅱ)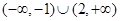 .
.试题分析:(Ⅰ)由于增函数的导数应大于等于零,故先对函数求导并令其大于零,可得
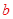 的取值范围,注意在求导时需细心;(Ⅱ)由函数在
的取值范围,注意在求导时需细心;(Ⅱ)由函数在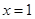 处取得极值可知,在
处取得极值可知,在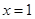 处函数导数为零,可求得
处函数导数为零,可求得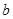 的值,要使
的值,要使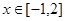 时,
时, 恒成立,需要求出
恒成立,需要求出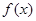 在
在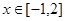 中的最大值,只有最大值小于
中的最大值,只有最大值小于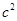 ,则
,则 恒成立,故可求得
恒成立,故可求得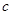 的范围,这类题目就是要求出
的范围,这类题目就是要求出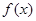 在给定区间上的最值.
在给定区间上的最值.试题解析:(1)
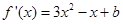 ,∵
,∵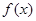 在
在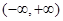 是增函数,
是增函数,∴
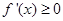 恒成立,∴
恒成立,∴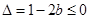 ,解得
,解得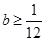 .
.∵
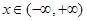 时,只有
时,只有 时,
时,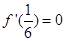 ,∴b的取值范围为
,∴b的取值范围为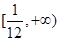 . 3分
. 3分(Ⅱ)由题意,
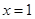 是方程
是方程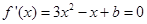 的一个根,设另一根为
的一个根,设另一根为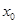 ,
,则
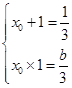 ∴
∴ ∴
∴ , 5分
, 5分列表分析最值:
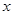 | 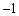 | 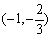 | 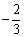 | 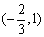 | 1 | 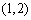 | 2 |
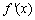 | | + | 0 | - | 0 | + | |
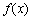 | 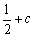 | 递增 | 极大值 | 递减 | 极小值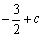 | 递增 | 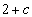 |
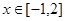 时,
时,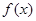 的最大值为
的最大值为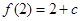 , 9分
, 9分∵对
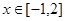 时,
时, 恒成立,∴
恒成立,∴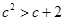 ,解得
,解得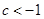 或
或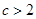 ,
,故
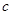 的取值范围为
的取值范围为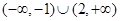 12分
12分
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
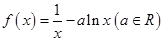 .
.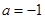 时,试确定函数
时,试确定函数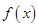 在其定义域内的单调性;
在其定义域内的单调性;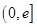 上的最小值;
上的最小值;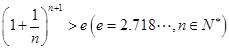 .
. ,(其中m为常数).
,(其中m为常数).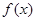 在区间
在区间 上的单调性;
上的单调性; .当
.当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 、
、 ,使得过
,使得过 、
、 点处的切线互相平行,求
点处的切线互相平行,求 的取值范围.
的取值范围.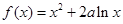 .
.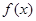 的图象在
的图象在 处的切线斜率为
处的切线斜率为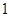 ,求实数
,求实数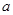 的值;
的值;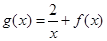 在
在 上是减函数,求实数
上是减函数,求实数 -
-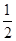 alnx,a∈R.
alnx,a∈R.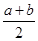 )≤
)≤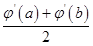 ≤φ′(
≤φ′(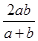 ).
). .
.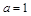 时,求函数
时,求函数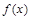 的单调增区间;
的单调增区间;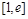 上的最小值.
上的最小值.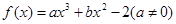 有且仅有两个不同的零点
有且仅有两个不同的零点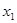 ,
,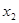 ,则( )
,则( ) 时,
时, ,
,
 ,
,
 时,
时,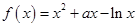 .
.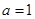 ,试求函数
,试求函数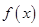 的单调区间;
的单调区间;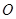 作曲线
作曲线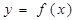 的切线,证明:切点的横坐标为1;
的切线,证明:切点的横坐标为1;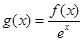 ,若函数
,若函数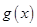 在区间(0,1]上是减函数,求
在区间(0,1]上是减函数,求 的取值范围.
的取值范围.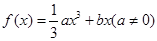 ,若f(3)="3f" ′(x0),则x0=( )
,若f(3)="3f" ′(x0),则x0=( )