题目内容
已知函数f(x)= -
-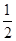 alnx,a∈R.
alnx,a∈R.
(Ⅰ)当f(x)存在最小值时,求其最小值φ(a)的解析式;
(Ⅱ)对(Ⅰ)中的φ(a),
(ⅰ)当a∈(0,+∞)时,证明:φ(a)≤1;
(ⅱ)当a>0,b>0时,证明:φ′(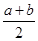 )≤
)≤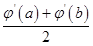 ≤φ′(
≤φ′(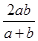 ).
).
 -
-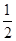 alnx,a∈R.
alnx,a∈R.(Ⅰ)当f(x)存在最小值时,求其最小值φ(a)的解析式;
(Ⅱ)对(Ⅰ)中的φ(a),
(ⅰ)当a∈(0,+∞)时,证明:φ(a)≤1;
(ⅱ)当a>0,b>0时,证明:φ′(
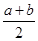 )≤
)≤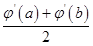 ≤φ′(
≤φ′(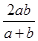 ).
).(Ⅰ)φ(a)=a-alna(a>0);(Ⅱ)详见解析.
试题分析:(Ⅰ)利用导数分析函数单调性,求最值;(Ⅱ)利用导数分析函数单调性,分类讨论.
试题解析:(Ⅰ)求导数,得f ′(x)=
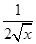 -
-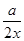 =
=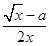 (x>0).
(x>0).(1)当a≤0时,f ′(x)=
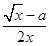 >0,f(x)在(0,+∞)上是增函数,无最小值.
>0,f(x)在(0,+∞)上是增函数,无最小值.(2)当a>0时,令f ′(x)=0,解得x=a2.
当0<x<a2时,f ′(x)<0,∴f(x)在(0,a2)上是减函数;
当x>a2时,f ′(x)>0,∴f(x)在(a2,+∞)上是增函数.
∴f(x)在x=a2处取得最小值f(a2)=a-alna.
故f(x)的最小值φ(a)的解析式为φ(a)=a-alna(a>0). 6分
(Ⅱ)由(Ⅰ),知φ(a)=a-alna(a>0),
求导数,得φ′(a)=-lna.
(ⅰ)令φ′(a)=0,解得a=1.
当0<a<1时,φ′(a)>0,∴φ(a)在(0,1)上是增函数;
当a>1时,φ′(a)<0,∴φ(a)在(1,+∞)上是减函数.
∴φ(a)在a=1处取得最大值φ(1)=1.
故当a∈(0,+∞)时,总有φ(a)≤1. 10分
(ⅱ)当a>0,b>0时,
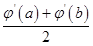 =-
=-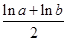 =-ln
=-ln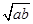 , ①
, ①φ′(
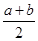 )=-ln(
)=-ln(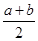 )≤-ln
)≤-ln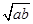 , ②
, ②φ′(
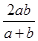 )=-ln(
)=-ln(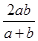 )≥-ln
)≥-ln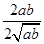 =-ln
=-ln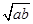 , ③
, ③由①②③,得φ′(
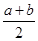 )≤
)≤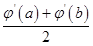 ≤φ′(
≤φ′(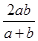 ). 14分
). 14分
练习册系列答案
相关题目
 ,
, 的图象经过
的图象经过 和
和 两点,如图所示,且函数
两点,如图所示,且函数 的值域为
的值域为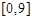 .过该函数图象上的动点
.过该函数图象上的动点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接 .
.
 的面积为
的面积为 ,求
,求 (其中
(其中 ).
). 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值; 时,函数
时,函数 上有且只有一个零点.
上有且只有一个零点.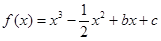 。
。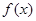 在
在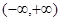 是增函数,求b的取值范围;
是增函数,求b的取值范围;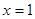 时取得极值,且
时取得极值,且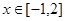 时,
时, 恒成立,求c的取值范围.
恒成立,求c的取值范围. (
( 是自然对数的底数).
是自然对数的底数). 在
在 处的切线也是抛物线
处的切线也是抛物线 的切线,求
的切线,求 的值;
的值; 时,是否存在
时,是否存在 ,使曲线
,使曲线 在点
在点 处的切线斜率与
处的切线斜率与 在
在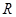 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由. ,
, .
. 为
为 的导函数,若不等式
的导函数,若不等式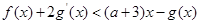 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围; ,对任意的
,对任意的 ,不等式
,不等式 恒成立.求
恒成立.求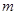 (
(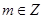 ,
, )的值.
)的值. 是实数,函数
是实数,函数 ,
, 和
和 ,分别是
,分别是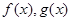 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 ,若函数
,若函数 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围; 且
且 ,若函数
,若函数 的最大值.
的最大值. 上的函数
上的函数 是最小正周期为
是最小正周期为 的偶函数,
的偶函数, 是
是 时,
时, ;当
;当 且
且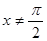 时,
时, .则函数
.则函数 在
在 上的零点个数为 .
上的零点个数为 . (
( 为非零常数).
为非零常数). 时,求函数
时,求函数 的最小值;
的最小值; 
 恒成立,求
恒成立,求 (其中
(其中 ),
), .
.