题目内容
已知函数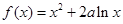 .
.
(1)若函数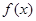 的图象在
的图象在 处的切线斜率为
处的切线斜率为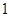 ,求实数
,求实数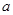 的值;
的值;
(2)在(1)的条件下,求函数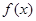 的单调区间;
的单调区间;
(3)若函数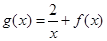 在
在 上是减函数,求实数
上是减函数,求实数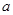 的取值范围.
的取值范围.
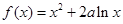 .
.(1)若函数
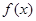 的图象在
的图象在 处的切线斜率为
处的切线斜率为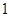 ,求实数
,求实数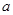 的值;
的值;(2)在(1)的条件下,求函数
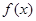 的单调区间;
的单调区间;(3)若函数
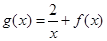 在
在 上是减函数,求实数
上是减函数,求实数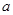 的取值范围.
的取值范围.(1) ;(2)函数
;(2)函数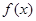 的单调递减区间是
的单调递减区间是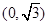 ;单调递增区间是
;单调递增区间是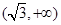 ;(3)
;(3) .
.
 ;(2)函数
;(2)函数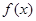 的单调递减区间是
的单调递减区间是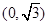 ;单调递增区间是
;单调递增区间是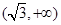 ;(3)
;(3) .
.试题分析:(Ⅰ)先求导数,再由函数
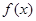 的图象在x=2处的切线的斜率为1,令
的图象在x=2处的切线的斜率为1,令 求解;(2)求出
求解;(2)求出 ,然后列表求出
,然后列表求出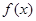 的单调区间;(3)求出
的单调区间;(3)求出 ,由函数
,由函数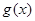 为
为 上的单调减函数,得出
上的单调减函数,得出 在
在 上恒成立,构造
上恒成立,构造 ,判断
,判断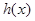 在
在 上为减函数,从而求解。
上为减函数,从而求解。试题解析:(1)
 1分
1分由已知
 ,解得
,解得 . 3分
. 3分(2)函数
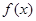 的定义域为
的定义域为 .
. .
. 当
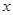 变化时,
变化时, 的变化情况如下:
的变化情况如下: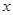 | 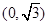 |  | 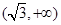 |
 | - |  | + |
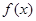 |  | 极小值 | 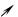 |
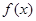 的单调递减区间是
的单调递减区间是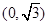 ;单调递增区间是
;单调递增区间是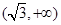 . 6分
. 6分(3)由
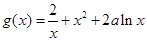 得
得 , 8分
, 8分由已知函数
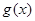 为
为 上的单调减函数,
上的单调减函数,则
 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立.
上恒成立.即
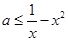 在
在 上恒成立. 10分
上恒成立. 10分令
 ,在
,在 上
上 ,
,所以
 在
在 上为减函数.
上为减函数. 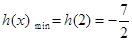 ,所以
,所以 . 14分
. 14分
练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 .
. 在区间
在区间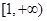 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围;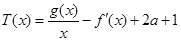 在区间
在区间 内有两个不同的零点(
内有两个不同的零点( 是自然对数的底数)?若存在,求出实数
是自然对数的底数)?若存在,求出实数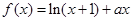 (
(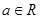 且
且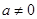 )
)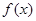 的单调性;
的单调性;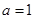 ,证明:
,证明: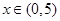 时,
时,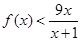 成立
成立 (
( ).
).  时,求函数
时,求函数 的单调区间;
的单调区间; 时,
时,
 上的最小值;
上的最小值;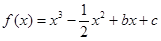 。
。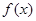 在
在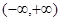 是增函数,求b的取值范围;
是增函数,求b的取值范围;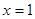 时取得极值,且
时取得极值,且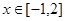 时,
时, 恒成立,求c的取值范围.
恒成立,求c的取值范围.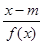 >
>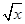 成立,求实数m的取值范围;
成立,求实数m的取值范围; ,
, .
. 为
为 的导函数,若不等式
的导函数,若不等式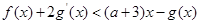 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围; ,对任意的
,对任意的 ,不等式
,不等式 恒成立.求
恒成立.求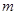 (
(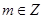 ,
, )的值.
)的值.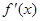 ,当
,当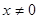 时,
时,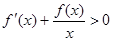 ,若
,若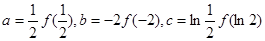 ,则下列关于a,b,c的大小关系正确的是( )
,则下列关于a,b,c的大小关系正确的是( ) 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为 .
. 的值;
的值; 根的个数,证明你的结论;
根的个数,证明你的结论; ,使得曲线
,使得曲线 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.