题目内容
【题目】第七届世界军人运动会于2019年10月18日至2019年10月27日在中国武汉举行,第七届世界军人运动会是我国第一次承办的综合性国际军事体育赛事,也是继北京奥运会之后我国举办的规模最大的国际体育盛会.来自109个国家的9300余名军体健儿在江城武汉同场竞技、增进友谊.运动会共设置射击、游泳、田径、篮球等27个大项、329个小项.经过激烈角逐,奖牌榜的前6名如下:
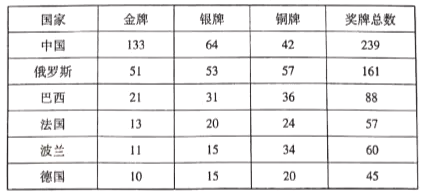
某大学德语系同学利用分层抽样的方式从德国获奖选手中抽取了9名获奖代表.
(1)请问这9名获奖代表中获金牌、银牌、铜牌的人数分别是多少人?
(2)从这9人中随机抽取3人,记这3人中银牌选手的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)从这9人中随机抽取3人,求已知这3人中有获金牌运动员的前提下,这3人中恰好有1人为获铜牌运动员的概率.
【答案】(1)金牌人数为2人、银牌人数为3人、铜牌人数为4人. (2)分布列见解析,![]() (3)
(3)![]()
【解析】
(1)分层抽样按比例计算各层抽取的人数;
(2)X的可能取值为0,1,2,3,计算出概率后可得分布列,由于银牌人数就是3人,由分布列计算期望.
(3)记事件A为“3人中有获金牌运动员”,事件B为“这3人中恰好有1人为获铜牌运动员”,求出![]() ,
,![]() ,然后由条件概率公式计算概率
,然后由条件概率公式计算概率![]() .
.
(1)由题意可知,德国获奖运动员中,金牌、银牌、铜牌的人数比为2:3:4,
所以这9名获奖运动员中金牌人数为2人、银牌人数为3人、铜牌人数为4人.
(2)X的可能取值为0,1,2,3,![]() ,
,
![]() ,
,
![]()
![]()
![]()
X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]()
(3)记事件A为“3人中有获金牌运动员”,事件B为“这3人中恰好有1人为获铜牌运动员”,
![]() ,
,
![]() ,
,
![]() .
.

【题目】一研学实践活动小组利用课余时间,对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查,月销售单价![]() (单位:元)和月销售量
(单位:元)和月销售量![]() (单位:百件)之间的一组数据如下表所示:
(单位:百件)之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 |
月销售单价 | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
月销售量 | 10 | 8 | 7 | 6 | 4 |
(1)根据1至5月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是1元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
(回归直线方程![]() ,其中
,其中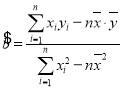 .参考数据:
.参考数据:![]() ,
,![]() )
)