Question

12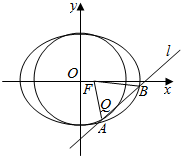．已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，点F为右焦点，直线1与圆x²+y²=3相切于点Q，且Q位于y轴的右侧，直线l交椭圆于相异两点A，B，如图所示，则|AF|+|AQ|的值为（　　）

• A． 4
• B． 1
• C． 2
• D． 3

Answer 1

分析 设A（x₁，y₁），（x₁＞0），连接OA，OQ，则|AQ|²=${x}_{1}^{2}+{y}_{1}^{2}-3$，|AF|²=${{（x}_{1}^{\;}-1）}^{2}+{y}_{1}^{2}$，结合${y}_{1}^{2}=3-\frac{{3{x}_{1}}^{2}}{4}$，化简可得答案．

解答 解：设A（x₁，y₁），（x₁＞0），
连接OA，OQ，在△OAQ中，|AQ|²=${x}_{1}^{2}+{y}_{1}^{2}-3$，
∵|AF|²=${{（x}_{1}^{\;}-1）}^{2}+{y}_{1}^{2}$，
又由${y}_{1}^{2}=3-\frac{{3{x}_{1}}^{2}}{4}$得：
|AQ|²=${\frac{1}{4}x}_{1}^{2}$，即|AQ|=$\frac{1}{2}$x₁，
|AF|²=${\frac{1}{4}x}_{1}^{2}-2{x}_{1}+4$，即|AF|=2-$\frac{1}{2}$x₁，
∴|AF|+|AQ|=2，
故选：C．

点评 本题考查的知识点是椭圆的简单性质，直线与圆锥曲线的关系，难度中档．