题目内容

4．若向量$\overrightarrow{a}$的一种正交分解是$\overrightarrow{a}$=λ1$\overrightarrow{{e}_{1}}$+λ2$\overrightarrow{{e}_{2}}$（λ1，λ2∈R），则正确的是（4）
（1）$\overrightarrow{{e}_{1}}$=$\overrightarrow{{e}_{2}}$（2）|$\overrightarrow{{e}_{1}}$|=|$\overrightarrow{{e}_{2}}$|（3）$\overrightarrow{{e}_{1}}$∥$\overrightarrow{{e}_{2}}$（4）$\overrightarrow{{e}_{1}}$⊥$\overrightarrow{{e}_{2}}$．

分析 根据$\overrightarrow{a}={λ}_{1}\overrightarrow{{e}_{1}}+{λ}_{2}\overrightarrow{{e}_{2}}$为向量$\overrightarrow{a}$的正交分解，从而便有$\overrightarrow{{e}_{1}}⊥\overrightarrow{{e}_{2}}$．

解答 解：∵是沿$\overrightarrow{{e}_{1}}，\overrightarrow{{e}_{2}}$方向上的正交分解；
∴$\overrightarrow{{e}_{1}}⊥\overrightarrow{{e}_{2}}$；
∴正确的是（4）．
故答案为：（4）．

点评 考查向量的正交分解的概念，清楚正交基的概念．

练习册系列答案
相关题目
14．函数f（x）=2x3-6x2+7在[-1，2]上的最大值是7．
15．下列命题中，判断正确的为（　　）
A．若两条平行直线中的一条平行于这个平面，则另一条也平行于这个平面
B．若直线a不平行于平面α，则α内一定不存在与a平行的直线
C．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β
D．若三角形ABC在平面α外，则边AB、BC、AC与面α的交点可能不在同一直线上
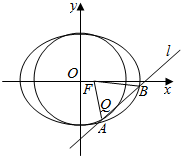12．已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，点F为右焦点，直线1与圆x2+y2=3相切于点Q，且Q位于y轴的右侧，直线l交椭圆于相异两点A，B，如图所示，则|AF|+|AQ|的值为（　　）
A．4B．1C．2D．3
19．直线y=1-x交椭圆mx2+ny2=1（m＞0，n＞0，且m≠n）于M、N两点，弦MN的中点为P，O为坐标原点，若直线OP的斜率为$\frac{1}{2}$，且以MN为直径的圆经过坐标原点，求椭圆的方程．
9．已知抛物线C1的焦点与椭圆C2：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{5}$=1的右焦点重合，抛物线C1的顶点在坐标原点，过点M（4，0）的直线l与抛物线C1分别相交于A、B两点．
（Ⅰ）写出抛物线C1的标准方程；
（Ⅱ）求△ABO面积的最小值．
16．若点P（2，4）在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，下列在椭圆上的点有：（1），（3），（4）
（1）P（-2，4）；
（2）P（-4，2）；
（3）P（-2，-4）；
（4）P（2，-4）
13．设A、B、C、D分别表示下列角的取值范围：
（1）A是直线倾斜角的取值范围；
（2）a是锐角；
（3）c是直线与平面所成角的取值范围；
（4）D是两异面直线所成角的取值范围，
用“⊆”把集合A、B、C、D连接起来得到B⊆D⊆C⊆A．
14．使奇函数f（x）=sin（2x+α）在[-$\frac{π}{4}$，0]上为减函数的α的值可以是（　　）
A．0B．$\frac{π}{2}$C．πD．$\frac{3}{2}$π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网